Test: Number system and Encoding Schemes - Grade 11 MCQ
15 Questions MCQ Test Computer Science for Grade 11 - Test: Number system and Encoding Schemes
The number of characters in 8 bit ASCII code (American Standard Code for Information Interchange) is
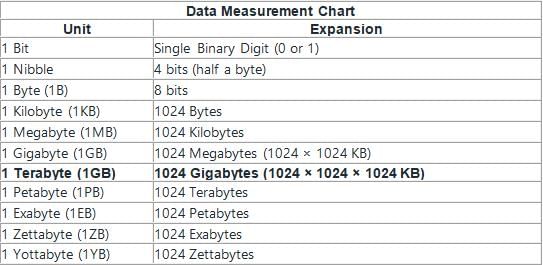
A movie requires 16 gigabytes of storage. How long will it take to download this movie, if the download speed is 64 megabytes per second? (1KB = 1024 Bytes)
Given below are two statements:
Statement I: The binary equivalent of decimal number (19)10 is (10101)2.
Statement II: (1011)2 + (110)2 = (10101)2
In light of the above statements, choose the correct answer from the options given below:
Statement I: The binary equivalent of decimal number (19)10 is (10101)2.
Statement II: (1011)2 + (110)2 = (10101)2
In light of the above statements, choose the correct answer from the options given below:
Given below are two statements:
Statement I: 8 megabytes = 213 gigabytes
Statement II: The decimal equivalent of the binary number (11101.101)2 is (29.625)10.
In the light of the above statements, choose the correct answer from the options given below:
A-F system is used in which of the following number systems?
The binary number 11000101 has ______ byte
Computer uses which number system to store data and perform calculations
Which of the following is the binary equivalent of the decimal number 35 ?
Given below are two statements
Statement I: The base of the binary number system is 2.
Statement II: Binary addition is just like decimal addition except that the rules are much simpler.
In light of the above statements, choose the correct answer from the options given below
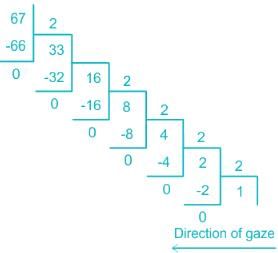
What is the binary equivalent of the decimal number 67.625?
What is the binary equivalent of decimal number 75?
The number of 8 bit strings that can be formed beginning with either “111...” or “101...” is
Find the correct pair from the following :
How many unique combinations of 0's and 1's can be made with a 5-binary-digit code?
|
84 videos|19 docs|5 tests
|