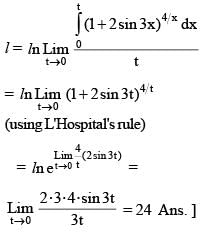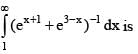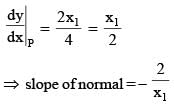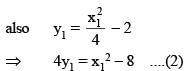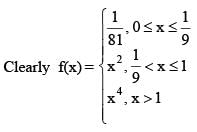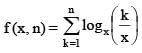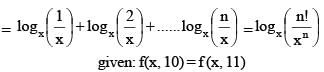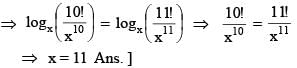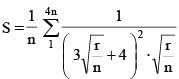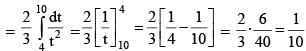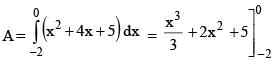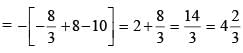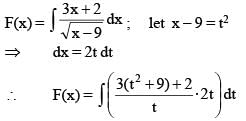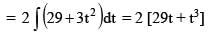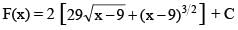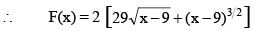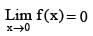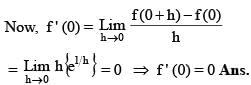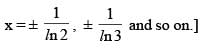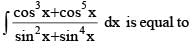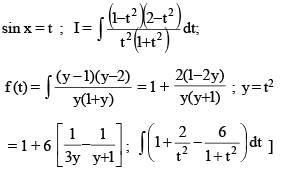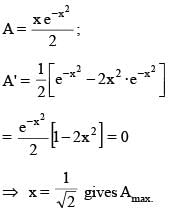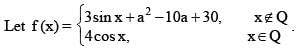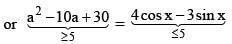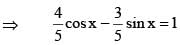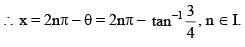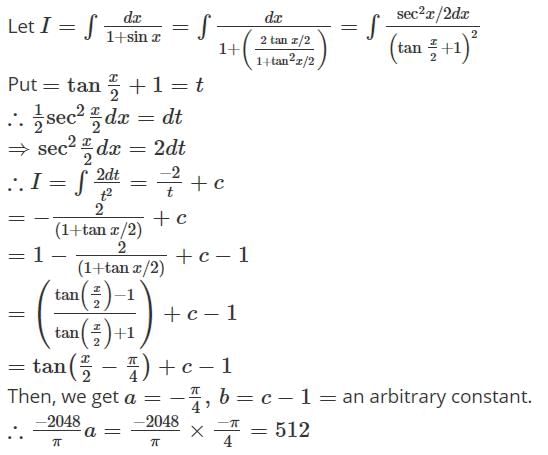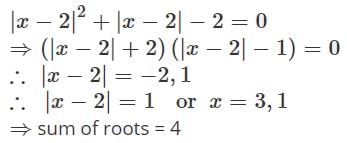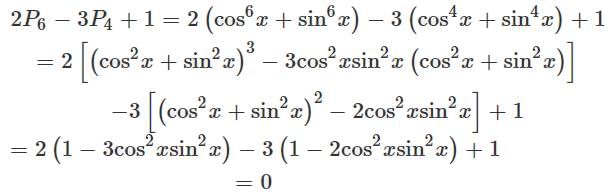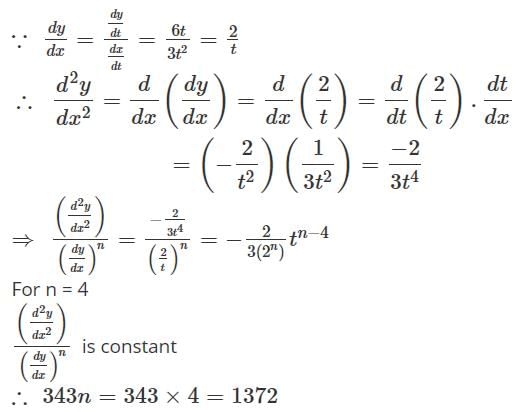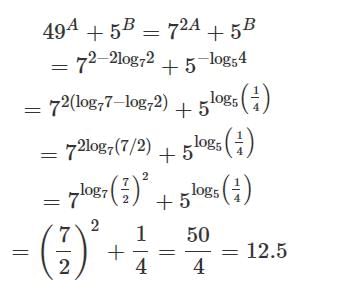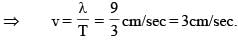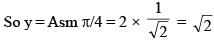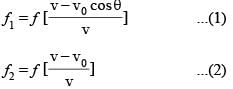JEE Main Practice Test- 14 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 14
Let f(x) be a one-to-one function such that f(1) = 3, f(3) = 1, f '(1) = – 4 and f '(3) = 2. If g = f –1, then the slope of the tangent line to 1/g at x = 1 is
If g (x3 + 1) = x6 + x3 + 2, then the value of g(x2 – 1) is
Suppose that f (0) = 0 and f ' (0) = 2, and let g (x) = f (- x + f (f (x))). The value of g ' (0) is equal to
A line L is perpendicular to the curve 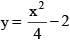 at its point P and passes through (10, –1). The coordinates of the point P are
at its point P and passes through (10, –1). The coordinates of the point P are

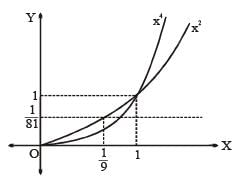
then the sum of the square of reciprocal of all the values of x where f(x) is non-differentiable, is equal to
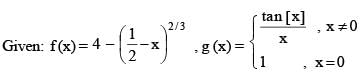
h(x) = {x},k(x) = 5log2 (x + 3) then in [0, 1], Lagranges Mean Value Theorem is NOT applicable to
[Note : where [x] and {x} denote the greatest integer and fractional part function of x respectively]
If the function f (x) = ax e–bx has a local maximum at the point (2, 10), then

then the value of x satisfying the equation f (x, 10) = f (x, 11), is
Number of integral solutions of the equation
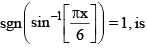
[Note : where [x] denotes the greatest integer less than or equal to x and sgn x denotes signum function of x.]
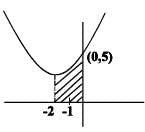
The area bounded by the curve y = x2 + 4x + 5 , the axes of co-ordinates & the minimum ordinate is
Number of roots of the equation x2 –2x–log2 |1 – x | = 3 is
Let F(x) be the primitive of 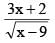 w.r.t. x. If F(10) = 60 then the value of F(13), is
w.r.t. x. If F(10) = 60 then the value of F(13), is
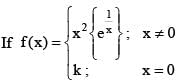
is continuous at x = 0, then
[Note : {x} denotes fractional part of x.]
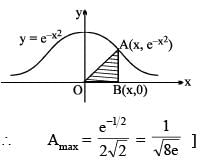
Point 'A' lies on the curve 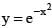 and has the coordinate
and has the coordinate 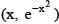 where x > 0. Point B has the coordinates (x, 0). If 'O' is the origin then the maximum area of the triangle AOB is
where x > 0. Point B has the coordinates (x, 0). If 'O' is the origin then the maximum area of the triangle AOB is
(Instruction to attempt numerical value (integer) type question: If your answer is 100 write 100 only. Do not write 100.0)
If 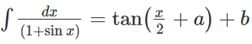 then the value of
then the value of 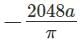 must be
must be
The sum of all the real roots of the equations
|x − 2|2 + |x − 2| − 2 = 0 is …..
If x = 2 + t3, y = 3t2 and 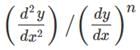 is a constant then the value of 343n must be
is a constant then the value of 343n must be
The value of 49A + 5B, where A = 1 - log72 and B = - log5 4 is
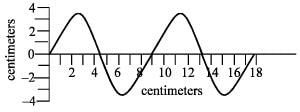
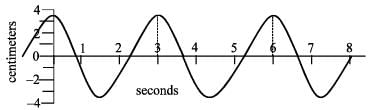
A transverse wave is travelling along a horizontal string. The first picture shows the shape of the string at an instant of time. This picture is superimposed on a coordinate system to help you make any necessary measurements. The second picture is a graph of the vertical displacement of one point along the string as a function of time. How far does this wave travel along the string in one second?
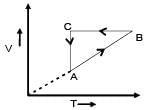
A cyclic process of an enclosed gas of constant mass is represented by volume (V) against absolute temperature (T) as shown. If P represents pressure, the graph representing the same process can be
A closed organ pipe is vibrating in its second overtone. The length of the pipe is 10cm and maximum amplitude of vibration of particles of the air in the pipe is 2mm. Then the amplitude of S.H.M. of the particles at 9cm from the open end is:
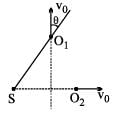
A sound source S and observers O1, O2 are placed as shown. S is always at rest and O1, O2 start moving with velocity v0 at t = 0. At any later instant, let f1 and f2 represent apparent frequencies of sound received by O1 and O2, respectively. The ratio f1/f2 is

Equal masses of three liquids A, B and C have temperatures 10oC, 25oC and 40oC respectively. If A and B are mixed, the mixture has a temperature of 15oC. If B and C are mixed, the mixture has a temperature of 30oC,. If A and C are mixed the mixture will have a temperature of
A steel rod is 4.000 cm in diameter at 30ºC. A brass ring has an interior diameter of 3.992 cm at 30ºC. In order that the ring just slides onto the steel rod, the common temperature of the two should be nearly (αsteel = 11 × 10-6/ºC and αbrass = 19 × 10-6/ºC)


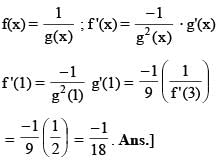
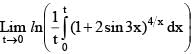 is equal to
is equal to