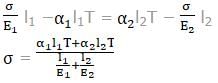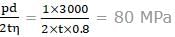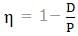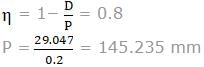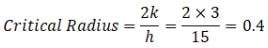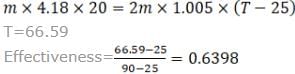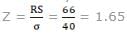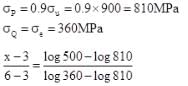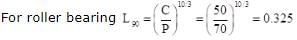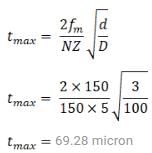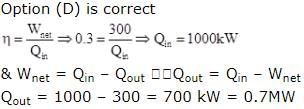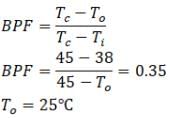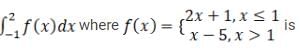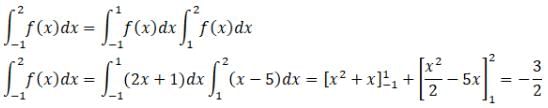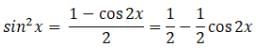Practice Test: Mechanical Engineering (ME)- 1 - Mechanical Engineering MCQ
30 Questions MCQ Test - Practice Test: Mechanical Engineering (ME)- 1
A vendor sells his articles at a certain profit percentage. If he sells his articles at 1/4th of his actual selling price then he incurs a loss of 60%. What is his actual profit percentage?
Direction: Read the following information carefully and answer the questions that follow:
The distribution of car sales of 6 companies has been shown in the pie chart below:

Note: The total number of cars sold is equal to 36000
If the average cost of a Hyundai car is 2 lakh rupees, then how much money is obtained by selling Hyundai cars?
The distribution of car sales of 6 companies has been shown in the pie chart below:

Note: The total number of cars sold is equal to 36000
If the average cost of a Hyundai car is 2 lakh rupees, then how much money is obtained by selling Hyundai cars?
Criteria for selecting candidate for internship programme
The candidate:
1) can preferably start the internship between 18th Oct'17 and 17th Nov'17
2) are preferably available for duration of 6 months
3) have computer skills and interest in designing
4) have already graduated or are currently in any year of study
5) knows to deal with customers
Nick is a high school student and wants to do an internship as his summer project. He is a very vibrant boy and goes well with people. Is he the right candidate for the internship?
The candidate:
1) can preferably start the internship between 18th Oct'17 and 17th Nov'17
2) are preferably available for duration of 6 months
3) have computer skills and interest in designing
4) have already graduated or are currently in any year of study
5) knows to deal with customers
Nick is a high school student and wants to do an internship as his summer project. He is a very vibrant boy and goes well with people. Is he the right candidate for the internship?
Direction: In the given question, one statement with a blank along with four words is given. Two of the given words can fit into the given blank. Five options with various combinations of these words are given. Choose the combination of the words that best fits into the blank.
Comedian Vasu Primlani takes hilarious ______ at the new trend of renaming Indian cities.
a) Jabs
b) Jokes
c) Satires
d) Gags
Which of the following is MOST OPPOSITE in meaning to Locus?
The ratio between the speed of a bus and train is 15 : 27, respectively. Also, a car covered a distance of 720 km in 9 h. the speed of the bus is three- fourth of the speed of the car. How much distance will the train cover on 7 h?
The Union Sports Ministry has approved five lakh rupees from the National Welfare Fund for Sportspersons for Kaur Singh who is suffering from heart disease. Kaur Singh is associated with which of the following sports?
Direction: In the following table data is given about a electronic shop. Some data is given and some data is hidden. Study the given data carefully and answer the related questions given below.
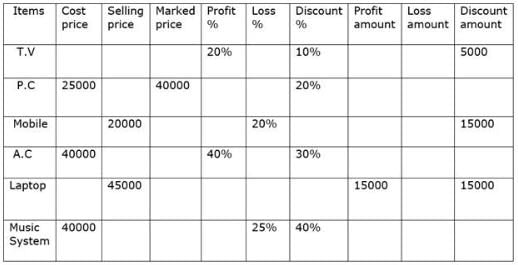
Selling price of T.V is what percent of Marked price of laptop ?
In below are given three statements followed by two conclusions numbered I and II. You have to take the given two statements to be true even if they seem to be at variance with commonly known facts and then decide which of the given conclusions logically follows from the statements, disregarding commonly known facts. Give answer
Statements: All pencils are papers.
All papers are black.
Conclusions: I. All black things being pencils is a possibility.
II. Some papers are not pencils.
Direction: In the given question, the 1st part of the sentence is given. The rest of the sentence/passage is split into four parts and named A, B, C and D. These four parts are not given in their proper order. Read the sentence and find out which of the four combinations is correct.
1) According to Indian Express, on Sunday, six men reached South Delhi businessman's house in Malviya Nagar in a Tata Safari car bearing the Haryana government’s sticker fixed on the windscreen.
A) One of the guys first took away all the cell phones of the businessman’s family members alleging that they had come on government duty to investigate a tax evasion charge.
B) The plan could have been successfully executed but one of the family members found their behaviour suspicious.
C) When the family member raised an alarm about the same, about 150 people from the same locality gathered outside the trader's house and the con men were beaten up and interrogated before they were handed over to the police.
D) They “searched” the house, moving from room to room, and collected Rs 20 lakh in cash that they kept in their cars.
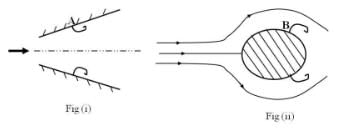
For flow of incompressible, viscous flow two configurations are shown. The inlet velocity for the diverging nozzle (Fig (i)) and free-stream velocity for flow past the bluff body (Fig(ii)) is constant and flow is laminar. The relation regarding velocity gradients at point A and B is (. Points A and B are separation points and y is the direction normal to the surface at the point of separation)
A pump is running at a speed of 4800 rpm and delivers 2.5 m3/s of water under a head of 20 m. The power input to a pump (in kW) at a shaft speed of 1600 rpm is (assume, pump efficiency = 85 %)
Figure shows a two composite bars AB and BC of equalcross sectional area are firmly attached at B. The outer end A and C are fixed to rigid supports. The coefficient of expansion of bar AB and BC are α1 and α2 and their modulus of elasticity are E1 and E2 respectively. The lengths are l1 and l2 respectively.
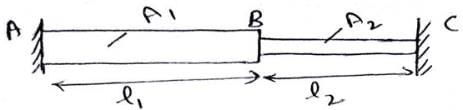
The stresses in both the bars due to a fall in temperature by T0C are
A 3 m diameter riveted boiler sustains an internal pressure of 1 MPa. The allowable safe stress of the material is 80 MPa. Take, diameter of rivet D = 6√t, where, t = plate thickness (in mm). The pitch of the single riveted but joint is (assume efficiency of the riveted joint = 80%)
A metallic ball in shape of sphere is made up of steel (thermal conductivity of 35W/m-K) of diameter 0.38 m . The outside heat transfer coefficient is 15W/m2. It is to be insulated with film of thermal conductivity 3W/m-K. The thickness of insulation should be
In a heat exchanger water enters at 90℃ and exits at 70℃. Air at entry temperature 25℃ flows at double the mass flow rate of water. The effectiveness of this heat exchanger is______
For a fluid with Prandtl number unity flowing over a flat plate, Reynolds Number is 450000, Nusselt Number is 900. The Surface friction coefficient will be
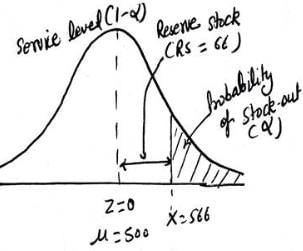
The demand for an item during the re-order period is normally distributed with mean = 500 units and standard deviation = 40 units.
Given data: Area between mean line and Z line corresponding to Z is given in table:

If the reserve stock is 66 units then the probability of stock-out of the units in the firm is
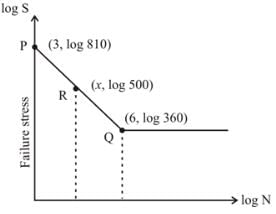
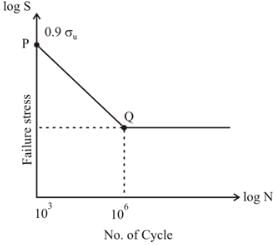
A cylindrical shaft has an ultimate strength (σu) of 900 MPa. The shaft has an endurance strength of of 360 MPa and alternating stress of 500 MPa, a log-log plot is shown in figure below. Calculate the shaft life ____ (In thousand)
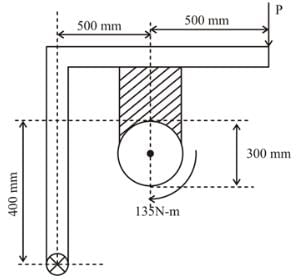
A single shoe block brake is shown in figure, drum diameter is 300 mm and = 0.3, the breaking torque is 135 N-m, Now which of the following conditions is true?
A Roller bearing has a basic dynamic load rating (C10 for 106 revolution) of 50 kN. If the equivalent radial load on the bearing in 70 kN, the expected life in (106 revolutions) is
In a plane milling operation following data has been taken as,
Length of workpiece = 150 mm
Cutter diameter = 100mm
No. of teeth = 5
Cutter speed = 150 rpm
Feed = 200 mm/min
Depth of cut = 3mm
Determine maximum undeformed chip thickness (in microns) ______.
The operation in which liquid is flown into voids by capillary action of a powder metallurgy product is known as
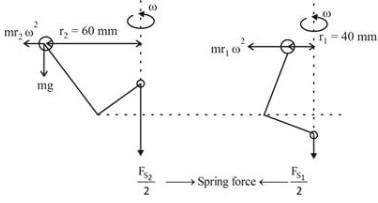
In a hartnell governor with the range of speed is zero, when the radius of rotation of mass of ball is 40mm the downward spring force is 120N and when the radius of rotation is 60mm the downward spring force is (in N)

Match the following:-
Column - I
A) Knife edge follower
B) Roller follower
C) Flat face follower
D) Radial follower
Column - II
(i) Wear is absent
(ii) Wear is highly reduced
(iii) Excessive wear
(iv) Line of motion passing from center of rotation
An engine operating at 30% efficiency produces work at a rate of 300 kW. The heat exhausted into the surrounding
Air after passing from a heating coil of temperature 45℃ is obtained at 38℃. Calculate inlet air temperature, if the bypass factor of the coil is 0.35.
There are two containers with one containing 5 red and 4 green ball and other containing 4 blue and 5 green balls. One ball is drawn at random from each container. The probability that one is red and another is blue
The Fourier cosine series for an even function g(x) is given as
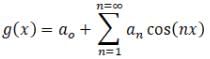
The value for coefficient a2 for g(x)=sin2x in interval [0,π] is