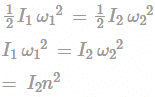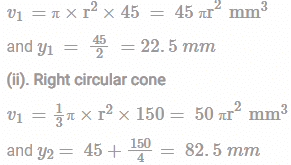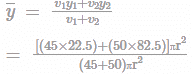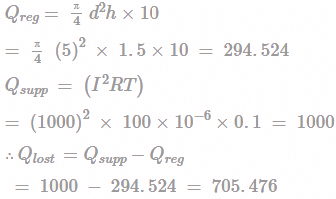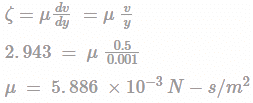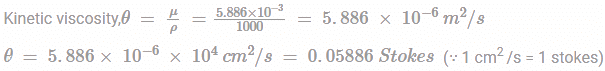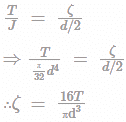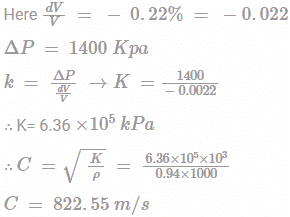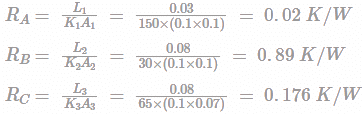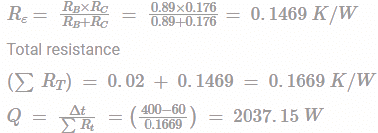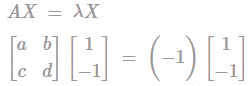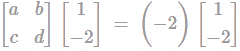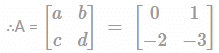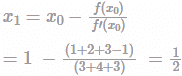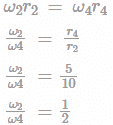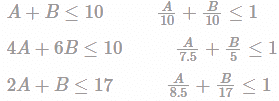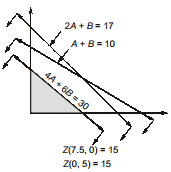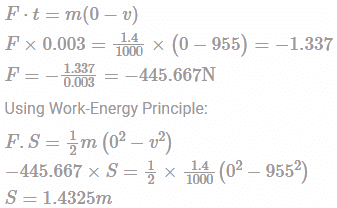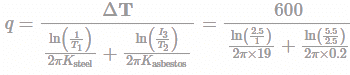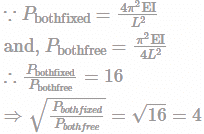Practice Test: Mechanical Engineering (ME)- 2
65 Questions MCQ Test GATE Mechanical (ME) 2023 Mock Test Series | Practice Test: Mechanical Engineering (ME)- 2
| 1 Crore+ students have signed up on EduRev. Have you? |
There are two lines made by joining points A, B,C. B lies between the line joining A and C. Is the distance between the A and C passes through the B more then 7 Km.
(i) The distance between A and B is 6 Km
(ii) Distance between B to C is 2 Km long,
From Statement I
We know the distance between Points B and C but we do not know about the distance between A and B
Statement II
This statement tells us about the distance between A and B and by using Both statement we can calculate the distance between A and C that is longer than the 2 Km.
Direction: In the given question, a word/phrase is given followed by three statements; I, II and III. Choose the pair of sentences which can be combined using the given word/ phrase when used at the beginning of the new sentence.
And
I: When Lionel Messi, Ronaldo and Neymar kick and dribble the football, they don’t remain confined to Argentina, Portugal or Brazil, respectively.
II: Let the entire world realise that through sports, especially football, we all can cement our bonds, wash away our bitterness and prejudices.
III: Live with a greater sense of closeness and joy with each other.
Here sentences II and III are displaying same sense that is realizing the benefit of football in our lives whereas sentence I is providing entirely different aspect of football as a sport.
Hence option (B) will be the most appropriate choice.
New sentence: Let the entire world realise that through sports, especially football, we all can cement our bonds, wash away our bitterness and prejudices, and live with a greater sense of closeness and joy with each other.
Which of the following is the MOST SIMILAR in meaning to Accreditation?
Certification = an official document attesting to a status or level of achievement.
Meticulous = showing great attention to detail; very careful and precise.
Lurid = very vividly shocking.
Suppressive = tending or acting to suppress.
Agreement = harmony or accordance in opinion or feeling.
In how many ways can you place 2 white bishops on an empty chess board?
Ways of doing that = 32C1 × 32C1
= 32 × 32 = 1024
Direction: In the question below are given statements followed by some conclusions. You have to take the given statements to be true even if they seem to be at variance with commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts.
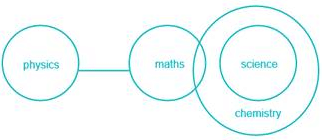
Statement:
No physics is maths.
Some chemistry is maths.
All sciences are chemistry.
Conclusion:
I. No science is physics.
II. Some physics are science.
III. Some physics are chemistry.
Conclusions:
I. No science is physics → False (It is possible but not definite).
II. Some physics are science → False (It is possible but not definite)
III. Some physics are chemistry → False (It is possible but not definite)
Conclusion I and II form complementary pair.
Hence, either conclusion I or II follows.
Direction: Read the information carefully and give the answer of the following questions-
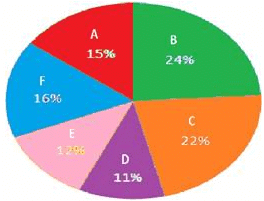
(This pie chart shows the percentage of students appear in six different exams in 2016)
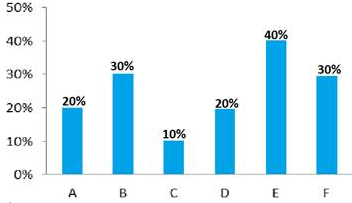
(This bar graph shows the percentage of failed students which appear in these six different exams in 2016)
If in 2016, total number of failed students in exam F was 4080, then how many passed students appears in the exam B?
14280 ( Let total number of students be = 100z.
Total number of students appears in exam F = 16% of 100z = 16z;
Total number of failed students in exam F = 30% of 16z = 4.8z = 4080;
=> z = 850;
Total number of passed students appears in the exam B = (100 – 30)% of 24% of 100z = 16.8z
= 16.8 × 850 = 14280 ;)
Direction: Two sentences with two blanks in each, followed by five alternatives with two words in each, are given. Choose that option as the answer which can fill both the blanks of both the sentences.
i. A sinking feeling of panic ________ over them and a temporary paralyzing fear engulfed them ________.
ii. Being a cleanliness freak, she ________ the floor and went down to the market only after the house was _________ clean.
In the following question, some statements followed by some conclusions are given. Taking the given statements to be true even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusions logically follows the given statements.
Statement:
Tension is detrimental to physical and mental health.
Conclusions:
I. To be healthy one should be free from tension.
II. Mental health depends upon the tension one experiences.
Conclusion II. Mental health depends upon the tension one experiences. (Follows).
Hence, option B is correct.
4 identical solid spheres are melted and reformed into a solid hemisphere. Then, the ratio of the curved surface area of the hemisphere to half of the surface area of a single sphere is -
Then, ATQ, Volume of Spheres = Volume of Hemisphere
4 x (4/3)πr3 = (2/3)πR3
Or, R / r = (8)1/3 = 2 …(1)
C.S.A of hemisphere = 2πR2
And, Surface area of sphere = 4πr2
ATQ, 2πR2 :( ½) of 4πr2
= 2πR2 :2πr2 = R2 :r2 {using (1)} ×
= 4 :1
A study of people who reduced the calories they consumed has found the strongest evidence yet that such restrictions slow down metabolism, raising hopes that a low calories lifestyle or treatments stimulating biological effects of restricted eating, could prolong health in old age. The report provides the most robust evidence to date that everything we have learnt in other animals can be applied to humans.
Which of the following argument will prove that the above conclusion is flawed?
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?
So equivalent moment of inertia w.r.t to first one = I1 + n2I2
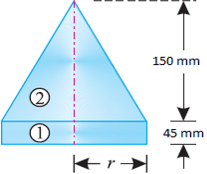
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?
(i). Cylinder
We know that distance between centre of gravity of the section and base of the cylinder
= 54.08 mm
Two steel sheet of 1 mm thick are resistance welded in a lap joint with a current of 10000 A for 0.1 sec. The effective resistance of joint can be taken as 100μΩ. The joint can be considered as cylinder φ5 of mm and 1.5 mm height. Ρsteel = 0.00786 g/mm3. The heat lost surroundings if the heat required to melt steel is 10 J/mm3 is?
A plate 1 mm distance from a fixed plate, is moving at 500 mm/s by a force induces a shear stress of 0.3 kg(f)/m2. The kinematic viscosity of the fluid (mass density 1000 kg/m3) flowing between two plates (in Stokes) is?
Using Newton’ law of viscosity,
For a circular shaft of diameter d subjected to torque T, the maximum value of the shear stress is?
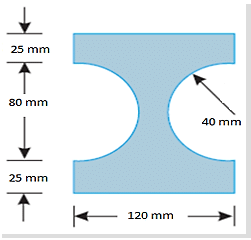
Figure shows the cross-section of a cast iron beam. Determine the moments of inertia of the section about horizontal axis passing through the centroid of the section.
Moment of inertia of the rectangular section about its horizontal axis passing through its centre of gravity, = bd3/12 = 120 x (130/2) = 21.97mm4 and moment of inertia of the circular section about a horizontal axis passing through its centre of gravity,
Moment of inertia of the whole section about horizontal axis passing through the centroid of the section,
IXX = (21.97 × 106) – (2.010 × 106) = 19.97 × 106 mm4
A liquid with specific gravity of 0.94 undergoes a reduction in volume of 0.22% when subjected to an increase in pressure of 1400kPa. The velocity of propagation of sound in this liquid will be ___________m/s
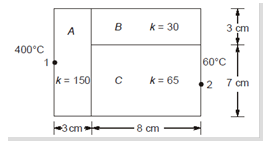
Heat flows through a composite slab as shown below, The depth of the slab is 10 cm. The k values are in W/m-K. The heat flow rate through the composite wall in W is?
Equivalent resistance between B and C-
A matrix has eigen values of ‒ 1 and ‒ 2 respectively. The corresponding eigen vectors are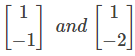 
respectively. The matrix is?
a -b = -1....(i)
c - d = 1.....(ii)
⇒ a - 2b = -2...(iii)
c - 2d = 4.....(iV)
From equation (i) and (iii), a = 0 and b = 1
From equation (ii) and (iv), c = - 2 and d = - 3
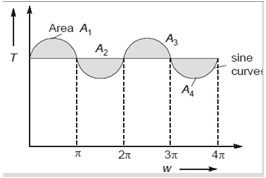
The turing moment diagram for engine is shown below.If the rotating parts have mass =50 kg, radius of gyration as 2.1 m and the fluctuation of speed is limited to 1.50% of mean speed on either side, find area A1 shaded as shown in figure[A1=A2=A3=A4].Angular speed is 50 rad/s.
emax=I ks ωavg2
I = m k2
I = 220.5×kgm2
emax = 220.5×ks×502 = 551250×Ks
Ks=1.5 % + 1.5% = 3%= 0.03
emax=551250×0.03
emax =16537.5 Nm/s
∴ A1=A2=A3=A4=16537.5 Nm/s
Newton-Raphson method is used to find the roots of the equation. x3+2x2+3x-1 =0If the initial guess is x0 = 1, then the value of x after 2nd iteration is _____?
x0 = 1
As per Newton-Raphson Method
Similarly
A thin cylinder of internal diameter 60 mm and wall thickness 2mm is subjected to an internal pressure of 1.25 N/mm2. The cylinder is also subjected to a torque of 60 Nm, the axis of the torque coinciding with that of the cylinder. The minor principal stress is MPa.
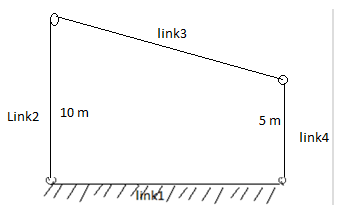
For the mechanism shown below Find the ratio of angular velocities of the link 2 and link 4.
Under such case the velocity end link 2 = velocity of end link 4
Consider the following linear programming problem:
Maximize Z =2A+3B, Subject to A+B ≤10, 4A+6B≤30, 2A+B≤17, A,B≥0
What can one say about the solution?
Maximum value of objective functions = 15 and it has alternative optimal solutions because of same constraint as objective function.
For the differential equation dy/dx + ay = 0 with y(0) = 1, solution is?
Taking integration on both sides, we get
or ln y = -ax+c
or y = 1, x = 0 follow initial condition.
ln 1 = -ax 0+c
∴ C = ln 1 = 0
So, ln y = -ax+C
ln y = -ax +0
∴y = e-at .
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.
In a JIT system, demand for a particular product is 2000 units. The safe stock is 15% of authorised inventory. The product spends 0.06 day in handling and 0.04 in processing. How many containers are to be authorised if 1 can contains 10 parts.
Safety stock = 0.15 × 200 = 30
No. of containers = (200+30)/10 = 23
A steel tube having inner radius 1 cm and outer radius 2.5 cm is covered with asbestos of thickness 3cm. the temperature difference between the outer surface of asbestos and inner surface of steel is 600°C. Ksteel=19w/m2k and Kasbestos= 0.2 w/m2k. Calculate the heat transfer rate per unit length of the pipe in W/m
Heat transfer rate q is given as
= 944.7 W/m
The sales of car in a showroom in first, second and third months are 70, 68 and 82 respectively. With the smoothing constant of 0.4, Find the forecast for the next month.
D1 = 70, D2=68, D3= 82 (given)
Note:- If initial forecasting is not given. you can assume it equal to the demand of that month.
Therefore, F1=70
Now according to formula given above,
F2= F1+α(D1-F1)= 70+0.4(70-70)= 70
F3= F2+α(D2-F2)= 70+0.4(68-70)= 69.2
Therefore, F4= F3+α(D3-F3)= 69.2+0.4(82-69.2)= 74.32
Square root of ratio of load required to buckle a column fixed on both ends to a column fixed on one end, free at other end is _____. The geometric length of both columns is same.
At point in a body stresses developed are such that σx =140MPa and σy = 60
MPa and the major principle stress is 150 MPa. What is the magnitude of max in-plane shear stress
σx=140MPaσy=60MPa
Let τmax be the max in plane shear stress.
We know that:
There is a car of mass m on a platform of mass M. The platform is kept on a smooth ice as shown in fig. If the car starts moving on the platform with a velocity V relative to platform then the velocity of platform recoil relative to ice is
Speed of car relative to platform = u+w
And according to question, V = u+w
So, the car velocity relative to ice, u = V – w
Assume the platform and car as a system, there is no external force acting on system i.e., linear momentum of system will be conserved. Initially there is no movement, so Initial linear momentum will be zero.
Initial linear momentum = Final linear momentum
0 = mu-Mw
0 = m (V-w)- Mw
w = mV/(M+m)
A bullet of mass m1=20 gm fired horizontally with a velocity of v=200 m/s hits a wooden block of mass m2 =500 gm (take g=9.8m/s2) resting on a horizontal plane as shown in the figure and the bullet remains embedded in the block after the impact. If the coefficient between the surfaces in contact remains constant at 0.3, the distance the block will move before coming to rest is:
The height of water level in a tank above the centre of a circular hole 2.5 cm in diameter is 50m. The velocity of water flowing through the hole is (neglect friction between jet and wall)
= √(2x9.81x50) = 31.32 m/s
Note:
The times to empty the same tank for two different starting heights, H1 and H2 is:
So, finally, if H2 = 2H1, as in the problem statement, then the time to empty the tank is not double, but √2 times longer.
Two blocks are connected by a light strings as shown in fig. The coefficient of friction at each surface is 0.25 and assumes the pulley is frictionless. The minimum value of m (in kg) for which system remain at rest is
At equilibrium
T=mgsinθ+μmgcosθ..........(i)
As pulley is frictionless so, the tension T will be same in whole string,
So,T+3×μgcosθ=3×gsinθ.............(ii)
Putting the values of μ and θ in (i) and (ii) and solved
The rigid bar AB, attached to two vertical rods as shown in figure, is horizontal before the load P is applied. The vertical movement(mm) of P is _____. Given P = 50 kN.
The solution of differential equation dy/dx = ex-y - x2e-y with y(0)=1 is
Electrical discharge machining or EDM, is a non-traditional method in which material is removed from a workpiece using thermal energy.
Q) ECM - i) Ion displacement
ECM is used to machine workpieces through the anodic dissolution of metal.
R) AJM- iv) Mechanical Erosion
The process makes use of an abrasive jet with high velocity, to remove material and provide smooth surface finish to hard metallic workpieces
S) LBM- ii) Amplified Radiation
It works on the principle that when a high energy laser beam strikes the surface of the work piece.
A wall of 0.5 m thickness is to be constructed from a material which has an average thermal conductivity of 1.4 W/m-K. The wall is to be insulated with a material having an average thermal conductivity of 0.35 W/m-K so that the heat loss per square metre will not exceed 1450 W. Assuming that the inner and outer surface temperature are 1200 °C and 15 °C respectively. The thickness of insulation required is ____ metre.
The blocks shown in the figure has 1 kg. The rear block moves with a speed of 2m/s towards the front block kept at rest. The spring attached to the front block is light and has a spring constant of 50 N/m. The maximum compression of the spring in meters is___
Using conservation of linear momentum,
Steam is condensing in a condenser at 100°C by a fluid which enter at 30°C and leaves at a higher temperature. The NTU of the heat exchanger is 3.2. Find the exit temperature of the fluid used for condensing steam in
Thi=The=100°C
Tci=30°C (The flow direction of fluid doesn’t have any effect in phase changing fluid HX)
ε=1-e-NTU
ε=1-e-3.2
ε=0.959
A casting of size 150 × 150 × 30 mm is not a side riser. The surface area of casting is 63000 mm2, having velocity of 2.14 m/s and volume flow rate as 0.245 m3/s. What would be the modulus of casting.
Therefore, Modulus of casting = Volume / Surface area
Volume of casting = 150 × 150 × 30 = 675000 mm3
Modulus of casting = 675000/63000 = 10.71
Note: Exothermic Riser Modulus is defined as the ratio of casting volume divided by the casting surface area. Normally, it is sufficient to calculate the modulus at the thickest section of the casting.
In a cooling tower, the DBT and WBT of air is 28°C and 23°C respectively while the temperature of water at inlet and outlet states is 32°C and 24°C respectively. The approach and range (in °C ) in cooling tower respectively is
Approach = 1°C
Range in cooling tower = Water temperature at the inlet states of cooling tower - water temperature at the exit states of cooling tower = 32 – 24
Range = 8°C
In a spring mass damper system (k=20N/m; m=2kg), The value of damped frequency (rad/sec) if the damper offers a resistance of 2N force when it vibrates with a constant velocity of 40cm/sec is:
x=40cmsec 0.4m/sec and F=2N
A cantilever beam with the bending moment M at the free end is shown in the diagram. The radius of Mohr’s circle of the element P is 7 MPa.What is the load (kN-m) applied at the free end?
A dealer for washing machines forecasts the demand at the rate of 600 units per month, for the next four months. The actual demand is found to be 500, 680, 800 and 900 units. The mean absolute deviation (MAD) and the BIAS are found to be
Find the value of number of standard normal variate for the critical path, If the project completion time is 19 days.
σ13=(7-1)/6=1
σ35=(14-2)/6=2
σ56=(15-3)/6=2
σcr=(12+22+22)(1/2)=3
Z(standard normal variate)
= (T - Tcp)/(σcr) = (19 - 17)/3 = 0.67
Blind holes of 20 mm diameter, 100 mm deep are being drilled in steel block. Drilling spindle speed is 600 rpm, feed is 0.2 mm/rev, point angle of drill is 135 °. During this operation, the drill wears out after producing 300 holes. Taylor’s tool life equation is of the form VT0.3 = C, where V = cutting speed in m/min and T = tool life in minutes Taylor’s constant C will be _____.
L1=Depth of the hole=100mm
L2=Approach length =0mm
L3=Length of tip=0.5D/tanθ =0.5×20/tan67.5°=4.14
(where,2θ=point angle or lip angle)
L4=Over travel=0mm
⇒L=L1+L3=104.142
In a single heater regenerative cycle (as shown in fig.), the 1 kg of steam enters the turbine at 25 bar, 400°C and the exhaust pressure is 0.1 bar. The feed water heater of direct contact type operates at 5 bar.
The values of enthalpies at different states are shown in table:
If the entropy at states 1, 4 and 6 are 6.9212 KJ/kgK, O.6493 KJ/kgK and 1.867 KJ/kgK respectively, then the increase in mean temperature of heat addition (in∘C) after heat regeneration is
Tm1 = 237.76°C
Mean temperature of heat addition without regeneration
Tm2 = 211.5°C
The increase in mean temperature of heat addition
Tm = 237.76-211.5 = 26.26°C
A rigid beam AB is supported as shown in figure. The rod AM is of steel, with a cross-sectional area of 10 cm2, the rod BN is of wood with a cross-sectional area of 100 cm2, the rod CD is of copper, and has cross-sectional area of 30 cm2. The displacement of the point of application of the load is [Take Es=200 G Pa, Ewood=10GPa] Young's modulus of copper =130 GPA
Ps+Pw=120kN
∑Ms=0
⇒3Ps=120×2
Both steel and wood plate get compressed by same length hence
δD= 0.4+0.2= 0.6mm.
A house that is losing heat at a rate of 60,000 kJ/hr when the outside temperature drops to 4 °C, is to be heated by electric resistance heaters. If the house is to be maintained at 24 °C at all times, then the irreversibility (in kW) of this process is
The reversible work is the minimum work required to accomplish this process, and the irreversibility is the difference between the reversible work and the actual electrical work consumed.
Actual power input
Woct'in = Qout = QH=60000 kj/h
=16.67 kW
COP of a reversible heat pump
=1.1225 kW
I=Woct.in - Wrev.in
=16.67-1.1225
=15.55 kW
If demand of a certain item doubles then the change in Economic Order Quantity is given as:
EOQnew = nEOQold
What will be the value of n?
Where R and I are ordering and inventory cost of 1 item,
This shows that: EOQ ∝ √U
21/2
A random variable X has probability density function f(x) as given below.
If the expected value E[X] = ⅔, then Pr [X < 0.5]="" />
If s is the stroke of follower, θo and θr being angular displacement of cam during outstroke and return stroke and ω is angular velocity of cam, then acceleration of the follower during return stroke will be:
Hence the average velocity of follower during outstroke = s/2 / to/2
= s/ to
= vomin + vomax/2
As vomin = 0, so
vomax = 2s / to
= 2ώs / θ0
Average velocity of follower during return stroke = s/2 / tr/2
= s/tr
= vrmin + vrmax/2
As vrmin = 0, so
vrmax = 2s / tr
= 2ώs / θr which is max velocity during return stroke.
Acceleration of the follower during outstroke = a0 = vomax / t0/2 = 4ώ2s / θ02
Acceleration of the follower during return stroke = ar = vrmax / t0/2 = 4ώ2s / θr2
ar = 4ώ2s / θr2
Two large parallel plates having temperatures T1 = 1500K and T2 = 500K are kept in such a way that radiation leaving from each surface is completely reached the 2nd surface. Emissivity values for plates are 0.5 and 0.25 respectively. Then heat transfer between the plates(in kW/m2)
Two large parallel plates,
temperatures T1 = 1500K
temperatures T2 = 500K
An increase in pressure of 500 kPa and decrease in volume by 0.02%, and Poisson ratio is 0.3. What is value of young modulus of elasticity?
K = 500 × 103/ (0.0002)
K = 2.5 × 109 Pa
µ = 0.3 (given)
as we know the relation
E = 3K (1- 2µ)
E = 3 × 2.5 ×109 (1- 2×0.3)
E = 3 × 109 Pa
Two very large parallel plane with emissivity’s 0.3 and 0.8 exchange radiative energy. The percentage reduction in radiative energy transfer when a polished aluminium radiation shield (∈=0.05) is placed between them is __________%.
Rate of radiation heat transfer with one shield
A radial load f1 = 5.6 kN acts for two hours on a rolling bearing and then reduces to f2 = 3.3 kN for one hour. The cycle then repeats itself. the shaft rotates at 300 rev/ min. What will be mean cubic load (fm), which should be used in rating the bearing for a life it 12,000 hour
= 2.905 kN
The weight of two people standing on a see saw at points A and B are measures 300N and 200N respectively. If the see saw is resting on its supports and weighs 500N, find the upward force P?
P + Q
= 300N + 500N + 200N
= 1000N
Now taking moments at point C due to Q, so clockwise moment will be:
= P x 4m
Also, anticlockwise moment will be:
= (300N x 5m) + (500N x 2m) + (200N x 1m)
= 2700Nm
Further, Clockwise Moment = Anticlockwise Moment
So: P x 4m = 2700Nm
P = 2700Nm/4
P = 675N
There is a vertical engine, having piston at the top and crank at the bottom, running at 2400 rpm. The length of crank and connectivity rod is 50 mm and 300 mm respectively. The diameter of the pistons is 100 mm and the mass of the reciprocating parts is 1.5 kg. The crank has turned 30 from the top dead centre during the expansion stoke and the gas pressure is 600 kN/m2. The net force on the piston is _____ N.
Length of crank, r = 50 mm = 0.05 m
Length of connecting rod, l = 300 mm = 0.3 m
N = 2400 rpm
Gas pressure, P = 600 kN/m2
Mass of reciprocating parts, m = 1.5 kg
Diameter of piston, d = 0.1 m
θ = 30o
Now,
n = l/r = 0.3/0.05 = 6
=4712.39 N
Inertia force, Fb = mrω2 (cos θ+ (Cos2θ/n))
Net force on the piston, F
F = Fp – Fb + mg = 4712.39 – 4497.59 + 1.5 x 9.81 =229.52 N ≈229 N
Let x and y be integers satisfying the following equations
2x2+y2 = 34
x + 2y = 11
The value of (x+y) is ________.
x + 2y = 11 .......(2)
From equation (2)
x = 11-2y now put the value of x in equation (1)....
2(11-2y)2 + y2 = 34
2 (121 + 4y2 + 44y) + y2 = 34
242 + 8 y2 -88y + y2 = 34
9 y2 - 88y + 208 = 0
On solving using Shridhar Acharya’s method we got
y = 4 & 52/9
Since, x +2y = 11
x = 11 - 8 = 3
So, x + y = 7
To compress a helical spring that is already compressed, where
Lo = 5.0 cm = 0.05 m
Li = 4.5 cm = 0.045 m
Lf = 3.5 cm = 0.035 m
k = 18,000 N/m
The work done will be:
x1 = Li − Lo = (0.045 m) − (0.05 m)
= −0.005 m
x2 = Lf − Lo = (0.035 m) − (0.05 m)
= −0.015 m
Step 2: Substitute the displacements (x1) and (x2) found in step 1 in Equation to give the work done as
Work1→2 = (1/2) k(x21 − x22)
= 1/2(18,000 N/m) × ((−0.005 m) 2 − (−0.015 m) 2)
= 1/2(18,000 N/m) × ((0.000025 − 0.000225) m2)
= 1/2(18,000 N/m)x (−0.0002 m2)
= −1.8 N · m = −180 N · cm
The negative sign on the work done means work was done on the spring.
A longitudinal copper tin (k=380 W/m-K) 600 mm long and 5 mm diameter is expose of air stream at 200C. The convective heat transfer coefficient is 20 W/m2-K. If the tin base temperature is 1500C, then efficiency of the tin __________%.
= 25.66%
A piston-cylinder device contains 0.05 m3 of gas initially at 180 kPa. At this stage, a linear spring that has a spring constant of 150 kN/m is just touching the piston but exerting no force on it. Now the heat is transferred to the gas, causing the piston to rise and to compress the spring until the volume inside the cylinder doubles. If the cross-sectional area of the piston is 0.25 m2, then the total work done (in kJ) by the gas will be
V2 = 2V = 2 × 0.05 = 0.1 m3
Displacement of the piston (and of the spring)
=0.5 m
Additional pressure applied by the spring on the gas at final state
=120 kPa
Without the spring, the pressure of the gas would remain constant at 180 kPa while the piston is rising. But under the effect of the spring, the pressure rises linearly from 180 kPa to 180 + 120 = 300 kPa at the final state
Total work done = Work done against the atmosphere + Work done against the spring
= Area I + Area II
= (300 + 180)/2 (0.1 - 0.05).
Alternate:
Total work done by the gas = Work done in expansion + Work saved in the form of potential energy of spring =180(0.1-0.05)+(½)×150×0.22=12 kJ
|
26 docs|239 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
26 docs|239 tests
|
Download free EduRev App
Related content with Practice Test: Mechanical Engineering (ME)- 2
|
|
Related tests with Practice Test: Mechanical Engineering (ME)- 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
