Test: Deflection of Beam,Bending Stress in Beam - 2 - Mechanical Engineering MCQ
30 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Test: Deflection of Beam,Bending Stress in Beam - 2
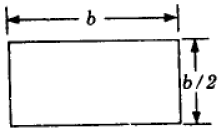
A beam cross-section is used in two different orientations as shown in the given figure: Bending moments applied to the beam in both cases are same. The maximum bending stresses induced in cases (A) and (B) are related as:

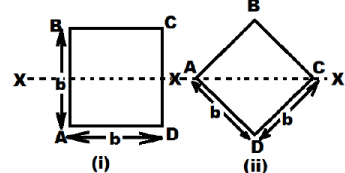
The ratio of the moments of resistance of a square beam (Z) when square section is placed (i) with two sides horizontal (Z1) and (ii) with a diagonal horizontal (Z2 ) as shown is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Assertion (A): For structures steel I-beams preferred to other shapes.
Reason (R): In I-beams a large portion of their cross-section is located far from the neutral axis.
A short column of symmetric cross-section made of a brittle material is subjected to an eccentric vertical load P at an eccentricity e. To avoid tensile stress in the short column, the eccentricity e should be less than or equal to:
The ratio of the core of a rectangular section to the area of the rectangular section when used as a short column is
A 0.2 mm thick tape goes over a frictionless pulley of 25 mm diameter. If E of the material is 100 GPa, then the maximum stress induced in the tape is:
A Cantilever beam of rectangular cross-section is 1m deep and 0.6 m thick. If the beam were to be 0.6 m deep and 1m thick, then the beam would.
Assertion (A): I, T and channel sections are preferred for beams.
Reason(R): A beam cross-section should be such that the greatest possible amount of area is as far away from the neutral axis as possible.
Assertion (A): A square section is more economical in bending than the circular section of same area of cross-section.
Reason (R): The modulus of the square section is less than of circular section of same area of cross-section.
A short vertical column having a square cross-section is subjected to an axial compressive force, centre of pressure of which passes through point R as shown in the above figure. Maximum compressive stress occurs at point
A simply supported beam carrying a concentrated load W at mid -span deflects by δ1 under the load. If the same beam carries the load W such that it is distributed uniformly over entire length and undergoes a deflection δ2 at the mid span. The ratio δ1: δ2 is
IES-1995; GATE-1994]
A cantilever beam of length L is subjected to a moment M at the free end. The moment of inertia of the beam cross section about the neutral axis is I and the Young’s modulus is E. The magnitude of the maximum deflection is
A triangular-shaped cantilever beam of uniformthickness is shown in the figure. The Young‟s modulus of the material of the beam is E. A concentrated load P is applied at the free end of the beam
The maximum deflection of the beam is
A cantilever of length L, moment of inertia I. Young's modulus E carries a concentrated load W at the middle of its length. The slope of cantilever at the free end is :
A cantilever beam of rectangular cross-section is subjected to a load W at its free end. If the depth of the beam is doubled and the load is halved, the deflection of the free end as compared to original deflection will be:
The safe stress for a hollow steel column which carries an axial load of 2100 kN is 125 MN/m2. if the external diameter of the column is 30cm, what will be the internal diameter?
The given figure shows a cantilever of span 'L' subjected to a concentrated load 'P' and a moment 'M' at the free end. Deflection at the free end is given by
Maximum deflection of a cantilever beam of length „l‟ carrying uniformly distributed load w per unit length will be:
[Where E = modulus of elasticity of beam material and I = moment of inertia of beam crosssection]
At a certain section at a distance 'x' from one of the supports of a simply supported beam, the intensity of loading, bending moment and shear force arc Wx, Mx and Vx respectively. If the intensity of loading is varying continuously along the length of the beam, then the invalid relation is:
A simply supported beam with width 'b' and depth ‟d‟ carries a central load W and undergoes deflection δ at the centre. If the width and depth are interchanged, the deflection at the centre of the beam would attain the value
Which one of the following is the correct statement?
If for a beam for its whole length, the beam is a cantilever:
By conjugate beam method, the slope at any section of an actual beam is equal to :
Two beams of equal cross-sectional area are subjected to equal bending moment. If one beam has square cross-section and the other has circular section, then
A beam with a rectangular section of 120 mm × 60 mm, designed to be placed vertically is placed horizontally by mistake. If the maximum stress is to be limited, the reduction in load carrying capacity would be
Assertion (A): A column subjected to eccentric load will have its stress at centroid independent of the eccentricity.
Reason (R): Eccentric loads in columns produce torsion.
A short column of external diameter D and internal diameter d carries an eccentric load W. Toe greatest eccentricity which the load can have without producing tension on the cross-section of the column would be:
For the configuration of loading shown in the given figure, the stress in fibre AB is given by :
Which one of the following combinations of angles will carry the maximum load as a column?
For the component loaded with a force F as shown in the figure, the axial stress at the corner point P is
If the area of cross-section of a circular section beam is made four times, keeping the loads, length, support conditions and material of the beam unchanged, then the qualities (List-I) will change through different factors (List-II). Match the List-I with the List-II and select the correct answer using the code given below the Lists
|
29 docs|220 tests
|
|
29 docs|220 tests
|



















