Thermodynamics & Power Plant - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Thermodynamics & Power Plant - 2
The e.m.f. in a thermocouple with the test junction at t°C on gas thermometer scale and reference junction at ice point is given by ε = 0.4 t2 − 15 × 10−4 t3 mv. The millivoltmeter is calibrated at ice and stream points. What will this thermometer read in a place where the thermometer reads 60°C
Pv diagram for n moles of an ideal gas is shown in figure
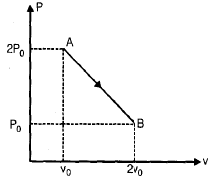
Q. The temperature volume graph will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An imaginary engine receives heat and does work on a slowly moving piston at such rates that the cycle of operation of 1 kg of working fluid can be represented as a circle 10 cm in diameter on a P-v diagram an which 1 cm = 300 kPa and 1 cm = 0.1 m3/kg. If the heat rejected by engine in a cycle is 1000 kJ/kg of working fluid, what will be its thermal efficiency?
Air at 101.325 kPa, 20° C is taken in to a gas turbine power plant at a velocity of 140 m/s through an opening of 0.15 m2 cross-section area. The air is compressed, heated, expanded through a turbine and at 0.18 MPa 150° C through an opening of 0.10 m2 cross-sectional area. The power output is 375 kw. The net amount of heat added to the air in kJ/kg is
A reversible heat engine operates between 600° C and 40° C. This engine drives a reversible refrigerator operating between 40° C and –18° C. Still there is a net work output of 3270 kJ. While the heat received by the engine by 2100 kJ. The cooling effect of refrigerator is
When the outside temperature is –10°C, a residential heat pump must provide 3.5 × 106 kJ per day to dwelling to maintain its temperature at 20°C. If the electricity costs Rs. 2.10 kWh, find the minimum operating cost for each day of operation.
In a Carnot cycle, heat is supplied at 350° C and rejected at 27° C. The working fluid is water which, while receiving heat, evaporates from liquid at 350° C to steam at 350° C. The associate entropy change is 1.44 kJ/kg K.
Q. If cycle operates on stationary mass of 1 kg of water, work done per cycle and heat supplied will be respectively
In a Carnot cycle, heat is supplied at 350° C and rejected at 27° C. The working fluid is water which, while receiving heat, evaporates from liquid at 350° C to steam at 350° C. The associate entropy change is 1.44 kJ/kg K.
Q.If the cycle operates in steady flow with a power output of 20 kW, then steam flow rate will be
A gas is compressed reversibly and adiabatically from state ‘a’ to state ‘b’. It is then heated at constant volume to state ‘c’. It is then taken through an isentropic process such that Tc = Td . It is then heated at constant pressure to state ‘e’ such that Tc = Te . Heat is then rejected reversibly from the gas at constant volume till it returns to state ‘a’. Take γ = 1.4.
Q. Ta in terms of Tb and Tc will be
A gas is compressed reversibly and adiabatically from state ‘a’ to state ‘b’. It is then heated at constant volume to state ‘c’. It is then taken through an isentropic process such that Tc = Td . It is then heated at constant pressure to state ‘e’ such that Tc = Te . Heat is then rejected reversibly from the gas at constant volume till it returns to state ‘a’. Take γ = 1.4.
Q. If Tb = 555 k and Tc = 8735 k then Ta would be
A steam boiler initial contains 5 m3 of steam and 5 m3 of water at 1 MPa. Steam is taken out at constant pressure unit 4m3 of water is left.
Given : at 1 MPa Vf = 0.001127 m3/kg Vg = 0.1944 m3/kg
Q. Mass of steam taken out of the boiler is
A steam boiler initial contains 5 m3 of steam and 5 m3 of water at 1 MPa. Steam is taken out at constant pressure unit 4m3 of water is left.
Given : at 1 MPa Vf = 0.001127 m3/kg Vg = 0.1944 m3/kg
Q. Heat transfer during the process will be
A platinum wire is used as a resistance thermometer the wire resistance was found to be 20 ohm and 36 ohm at ice point and steam point respectively and 40 ohm at melting point of antimony 630.50°C.
Find the resistance of wire of 70°C. If the resistance varies with temperature by the relation R = R0 (1 + at + b2)
A water chilling plant remove heat from the water at a rate of 42 MJ/h. Heat leaks in to the water from surrounding at an average rate of 4.2 MJ/h. The time required for cooling a batch for 1500 kg of water from 40° C to 10° C, is _________ hours. (C p = water 4.2 kJ/kgk)
In a vessel, 10 kg of O2 is heated in a reversible now flow, constant volume process so that the pressure of O2 is increased two times of initial value. If the initial temperature is 20°C what will be the internal energy change (Cv = 0.65 kJ/kg k).
Suppose 1g of water vaporizes isobarically at atmospheric pressure (1.01 × 105 Pa). Its volume in liquid state is 1 cm3 and in vapour state is 1671 cm3. Find the change in internal energy of system. (Latent heat of vaporization = 2.96 × 196 J/kg).
Air at a flow rate of 1 kg/s enters the nozzles of a jet engine at a temperature of 200 kPa and at a velocity of 50 m/s. It leaves nozzle at a temperature of 650 k and pressure of 100 kPa. Heat loss at a constant rate of 25 kw takes place from the nozzle to the surroundings. Assume air to behave as ideal gas with the constant pressure specific heat values of 1.005 kJ/kg and neglect potential energy change, the exit velocity of air is _________ m/s.
A heat pump working on the Carnot cycle takes in heat from a reservoir at 5°C and delivers heat to a reservoir at 60°C. The heat pump is driven by a reversible heat engine which takes heat to a reservoir at 60° C. The reversible heat engine also drives a machine that absorbs 30 kW. If the heat pump extracts 17 kJ/s from the 5°C reservoir, then
Q. Determine the rate of heat supply from 8400° C source
A heat pump working on the Carnot cycle takes in heat from a reservoir at 5°C and delivers heat to a reservoir at 60°C. The heat pump is driven by a reversible heat engine which takes heat to a reservoir at 60° C. The reversible heat engine also drives a machine that absorbs 30 kW. If the heat pump extracts 17 kJ/s from the 5°C reservoir, then
Q. Determine the rate of heat rejection to 60° C sink
|
29 docs|220 tests
|
|
29 docs|220 tests
|

















