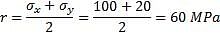Test: Principal Stress & Strain - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Test: Principal Stress & Strain - 1
A block of steel is loaded by a tangential force on its top surface while the bottom surface is held rigidly. The deformation of the block is due to
The figure shows the state of stress at certain point in a stresses body. The magnitudes of normal stresses in x and y direction are 100 MPa and 20 MPa respectively. The radius of Mohr’s stress circle representing this state of stress is


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
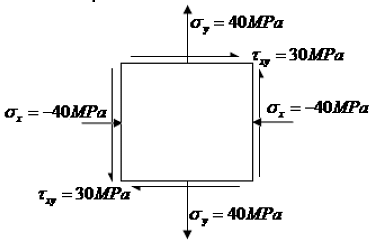
The state of stress at a point in a loaded member is shown in the figure. The magnitude of maximum shear stress is [1MPa = 10 kg/cm2]
In a bi-axial stress problem, the stresses in x and y directions are (σ x = 200 MPa and σy =100 MPa. The maximum principal stress in MPa, is:
The normal stresses at a point are σx = 10 MPa and, σy = 2 MPa; the shear stress at this point is 4MPa. The maximum principal stress at this point is:
The state of stress at a point under plane stress condition is
σxx = 40 MPa , σyy = 100 MPa and τxy = 40 MPa .
The radius of the Mohr‟s circle representing the given state of stress in MPa is
When a component is subjected to axial stress the normal stress σn is maximum, if cos θ is _______ . (σn=σxCos2θ)
1. maximum
2. minimum
3. always one
4. always zero
If the two principal strains at a point are 1000 × 10-6 and -600 × 10-6, then the maximum shear strain is:
In the case of bi-axial state of normal stresses, the normal stress on 45° plane is equal to
In a two-dimensional problem, the state of pure shear at a point is characterized by
For the state of stress of pure shear τ the strain energy stored per unit volume in the elastic, homogeneous isotropic material having elastic constants E and ν will be:
Assertion (A): Circular shafts made of brittle material fail along a helicoidally surface inclined at 45° to the axis (artery point) when subjected to twisting moment.
Reason (R): The state of pure shear caused by torsion of the shaft is equivalent to one of tension at 45° to the shaft axis and equal compression in the perpendicular direction.
The state of plane stress in a plate of 100 mm thickness is given as σxx = 100 N/mm2, σyy = 200 N/mm2, Young's modulus = 300 N/mm2, Poisson's ratio = 0.3. The stress developed in the direction of thickness is:
Consider the following statements:
State of stress in two dimensions at a point in a loaded component can be completely specified by indicating the normal and shear stresses on
1. A plane containing the point
2. Any two planes passing through the point
3. Two mutually perpendicular planes passing through the point
Of these statements
In a strained material one of the principal stresses is twice the other. The maximum shear stress in the same case is tmax . Then, what is the value of the maximum principle stress?
The principal stresses σ1, σ2 and σ3 at a point respectively are 80 MPa, 30 MPa and –40 MPa. The maximum shear stress is:
Plane stress at a point in a body is defined by principal stresses 3σ and σ. The ratio of the normal stress to the maximum shear stresses on the plane of maximum shear stress is:
For the state of plane stress.
Shown the maximum and minimum principal stresses are:
Two-dimensional state of stress at a point in a plane stressed element is represented by a Mohr circle of zero radius. Then both principal stresses
|
29 docs|220 tests
|
|
29 docs|220 tests
|