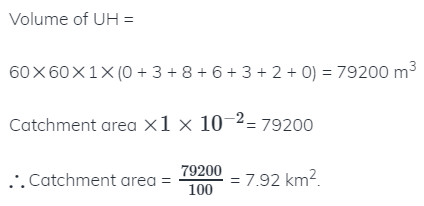Practice Test: Gate Civil Engineering(CE) 2017 Paper - GATE MCQ
30 Questions MCQ Test - Practice Test: Gate Civil Engineering(CE) 2017 Paper
Consider the following sentences: All benches are beds. No bed is a bulb. Some bulbs are lamps. Which of the following can be inferred?
i. Some beds are lamps.
ii. Some lamps are beds.
ii. Some lamps are beds.
The following sequence of numbers is arranged in increasing order: 1, x, x, x, y, y, 9,16,18.
Given that the mean and median are equal, and are also equal to twice the mode, the value of y is
The bacteria in milk are destroyed when it _________ heated to 80 degree Celsius.
If the radius of a right circular cone is increased by 50%, its volume increases by
__________ with someone else’s email account is now very serious offence.
The last digit of (2171)7 + (2172)9 + (2173)11 + (2174)13 is
Two machines M1 and M2 are able to execute any of four jobs P, Q, R and S. The machines can perform one job on one object at a time. Jobs P, Q, R and S take 30 minutes, 20 minutes, 60 minutes and 15 minutes each respectively. There are 10 objects each requiring exactly 1 job. Job P is to be performed on 2 objects. Job Q on 3 objects. Job R on 1 object and Job S on 4 objects. What is the minimum time needed to complete all the jobs?
Students applying for hostel rooms are allotted rooms in order of seniority. Students already staying in a room will move if they get a room in their preferred list. Preferences of lower ranked applicants are ignored during allocation.
Given the data below, which room will Ajit stay in?
The bar graph below shows the output of five carpenters over one month, each of whom made different items of furniture: Chairs, tables, and beds.
Consider the following statements.
i. The number of beds made by carpenter C2 is exactly the same as the same as the number of tables made by carpenter C3.
ii. The total number of chairs made by all carpenters is less than the total number of tables. Which one of the following is true?
The old concert hall was demolished because of fears that the foundation would be affected by the construction tried to mitigate the impact of pressurized air pockets created by the excavation of large amounts of soil. But even with these safeguards, it was feared that the soil below the concert hall would not be stable.
From this, one can infer that
The ordinates of a 2 – h unit hydrograph at 1 hour intervals starting from time t = 0, are 0, 3, 8, 6, 3, 2 and 0 m3/s. Use trapezoidal rule for numerical integration, if required.
What is the catchment area represented by the unit hydrograph?
A uniformly distributed line load of 500 kN/m is acting on the ground surface. Based on Boussinesq’s theory, the ratio of vertical stress at a depth 2 m to that at 4 m, right below the line of loading, is
According to IS 456-2000, which one of the following statements about the depth of neutral axis χu,bal for a balanced reinforced concrete section is correct?
Group I lists the type of gain or loss of strength in soils.
Group II lists the property or process responsible for the loss or gain of strength in soils.
Group I Group II
P. Regain of strength with time 1. Boiling
Q. Loss of strength due to cyclic loading 2. Liquefaction
R. Loss of strength due to upward seepage 3. Thixotropy
S. Loss of strength due to remolding 4. Sensitivity
The correct match between Group I and Group II is
A runway is being constructed in a new airport as per the International Civil Aviation Organization (ICAO) recommendations. The elevation and the airport reference temperature of this airport are 535 m above the mean sea level and 22.65°C, respectively. Consider the effective gradient of runway as 1%. The length of runway required for a design-aircraft under the standard conditions is 2000 m. Within the framework of applying sequential corrections as per the ICAO recommendations, the length of runway corrected for the temperature is
A soil sample is subjected to a hydrostatic pressure, σ. The Mohr circle for any point in the soil sample would be
The figure shows a two-hinged parabolic arch of span load of intensity q per unit length.
The maximum bending moment in the arch is equal to
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is
Two machines M1 and M2 are able to execute any of four jobs P, Q, R and S. The machines can perform one job on one object at a time. Jobs P, Q, R and S take 30 minutes, 20 minutes, 60 minutes and 15 minutes each respectively. There are 10 objects each requiring exactly 1 job. Job P is to be performed on 2 objects. Job Q on 3 objects. Job R on 1 object and Job S on 4 objects. What is the minimum time needed to complete all the jobs?
The number of parameters in the univariate exponential and Gaussian distributions, respectively, are
The wastewater form a city, containing a high concentration of biodegradable organics, is being steadily discharged into a flowing river at a location S. If the rate of aeration of the river water is lower than the rate of degradation of the organics, then the dissolved oxygen of the river water
The reaction rate involving reactants A and B is given by −k [A]α [B]β. Which one of the following statements is valid for the reaction to be first –order reaction?
A strip footing is resting on the ground surface of a pure clay bed having an undrained cohesion Cu. The ultimate bearing capacity of the footing is equal to
A simply supported beam is subjected to a uniformly distributed load. Which one of the following statements is true?
A triangular pipe network is shown in the figure.
The head loss in each pipe is given by hf = rQ1.8, with the variables expressed in a consistent set of units. The value of r for the pipe AB is 1 and for the pipe BC is 2. If the discharge supplied at the point A (i.e., 100) is equally divided between the pipes AB and AC, the value of r (up to two decimal places) for the pipe AC should be_______.
A super-elevation e is provided on a circular horizontal curve such that a vehicle can be stopped on the curve without sliding. Assuming a design speed v and maximum coefficient of side friction fmax, which one of the following criteria should be satisfied?
Which one of the following is NOT present in the acid rain?
The accuracy of an Electronic Distance Measuring Instrument (EDMI) is specified as ± (a mm + b ppm). Which one of the following statements is correct?
Consider the following partial differential equation: