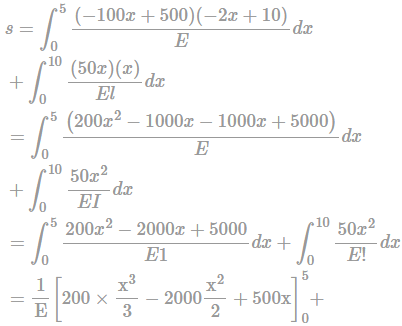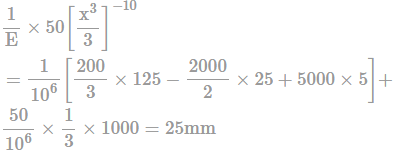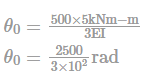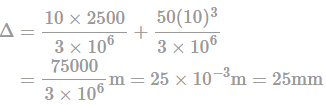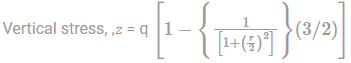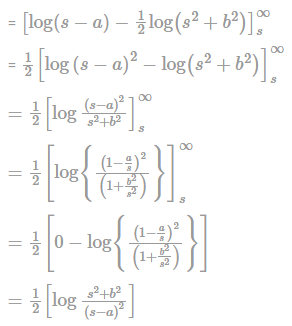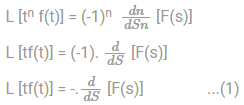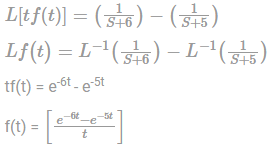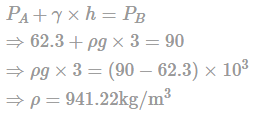Practice Test: Civil Engineering (CE)- 11

The simple interest on a certain sum for 2 years at 9% per annum is Rs. 225 less than the compound interest on the same sum for 2 years at 10% per annum. The sum is:

Which of the following is the MOST OPPOSITE in meaning to Obstreperous?

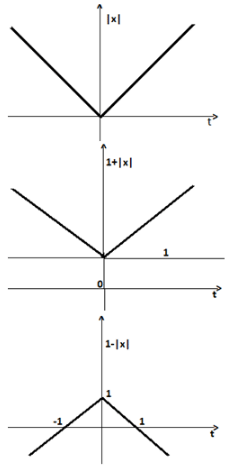
Consider a function f(x)=1-|x| on -1≤x≤1.The value of x at which the function attains a maximum, and the maximum value of function are:((mathematics:maxima,minima)

An article is sold with a certain profit percentage such that selling the same at one-third price, there will be a loss of 60%. Find the certain profit percentage.

Rs. 200 are divided among Arun, Bholu and Chetan such that Arun's share is Rs. 30 more than Bholu's and Rs. 20 less than Chetan's. What is Bholu's share?

Average marks in a test conducted in a class of 24 students gave the average score as 56. It was detected that while computing the average, marks of 3 students were taken as 46, 47 and 43 instead of 64, 74 and 34 respectively. Which of the following is the most appropriate description of the percentage by which the class average goes up now?

Present average age of Kanika and Shweta is ‘x’ years. Ratio of the age of Kanika one year ago to the age of Monika four year hence will be 1: 2. Present average age of Kanika, Monika and Shweta is 22 years. Find the value of ‘x’ if the present age of Kanika is 16 years.

The dip of the compass needle ______.

The Sludge Volume Index for mixed liquor having suspended solids concentration of 2000 mg/l and showing a settled volume of 200 ml from a one-litre sample would be

The velocity field for flow is given by

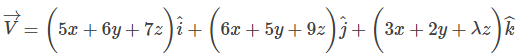
and the density varies as p = p_o exp (-2t). In order that the mass is conserved, the value of λ should be;

In the influence line diagram for mid-span bending moment of a simply supported beam, the ordinate at the quarter span is 0.5 m. If the span of the beam is doubled, the ordinate at the mid-span of the influence line will be;

The incorrect statements is/are;

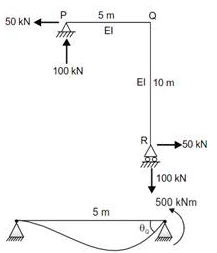
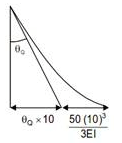
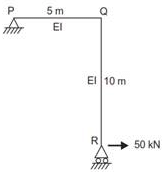
A portal frame shown in figure (not drawn to scale) has a hinge support at joint P and a roller support at joint R. A point load of 50 kN is acting at joint R in the horizontal direction. The flexural rigidity. EI, of each member is 106 kNm2. Under the applied load, the horizontal displacement (in mm, round off to 1 decimal place) of joint R would be __________

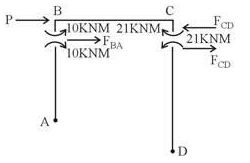
A plane frame is as shown in the figure below. If MBA = 10 kNM (clockwise) and MCD = 21 kNM (counter clockwise) then the value of load P is

A circular tank of base diameter 12m is subjected to a total load of 12,000 kN. Calculate the vertical stress (in kN/m²) at a point P which is at a depth of 3m and 2m away from the centre of the loaded area.

The results of two plate load tests performed on a given location with two circular plates are given below:

1. Diameter = 750 mm, S = 15 mm, Q = 150 kN

2. Diameter = 300 mm, S = 15 mm, Q = 50 kN

Use Housel’s equation i.e. Q = Aq + Ps

A = contact area

q = bearing pressure beneath area A (constant)

P = perimeter of footing

s = Perimeter shear (constant)

Determine the load (in kN) on circular footing 1.2 m diameter that will cause a settlement of 15 mm.

The net safe bearing capacity of a purely cohesive soil

A scale representing either three units or only one unit and its fractions up to second place of decimal point is _______.

If f(t) = (e^at - cos bt) 1/t , then the Laplace transform of f(t)

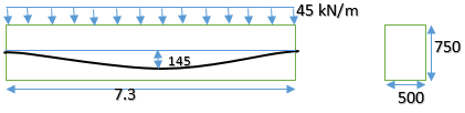
A concrete beam pre-stressed with a parabolic tendon is shown in the fig. The pre-stressing force applied is 1620 kN. The ULD includes self-weight of the beam. The stress in the top fibre of the middle section is (take compressive stress as positive)

Consider a signal x (t) given by x(t) L.T. ↔ x(s) = log(s+5/s+6) , then x(t) is given by

Consider the following simultaneous equations (with c₁, and c₂ being constants):

3x₁ + 2x₂ = c₁

4x₁ + x₂ = c₂

The characteristic equation for these simultaneous equations is;

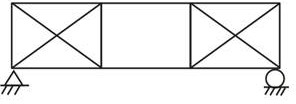
The degree of static indeterminacy of the truss shown below is.

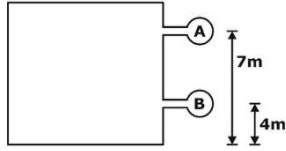
A pressure gauge reads 62.3 kPa and 90 kPa respectively at heights of 7 m and 4 m fitted on the side of a tank filled with liquid. What is the approximate density of the liquid on kg/m³?

Which one of the statement is INCORRECT in design of hourly traffic volume?

A lift irrigation scheme using a discharge of 81m³/hr is planned to raise a crop whose delta is 45cm. Intensity of irrigation is 55%. Assuming 4500 hours of working of water supply for a year, area(hectares) required for irrigation would be;

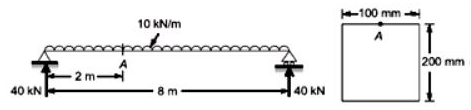
An 8 m long simply-supported elastic beam of rectangular cross-section 100mm × 200 mm is subjected to a uniformly distributed load of 10 kN/m over its entire span. The maximum principal stress (in MPa, up to two decimal places) at a point located at the extreme compression edge of a cross-section and at 2 m from the support is ____________.

The anchorage value of a standard bend, of a reinforcement bar of diameter φ

What is the anchorage length of a tie bar, which is bent through 135° round a bar of diameter 12mm?

If two centrifugal pumps (I and II) with heads H₁, H_II and discharge Q₁, Q_II are connected in series, then the correct option is:

A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m³. The highest flood in the river is 12000 m³/s. the corresponding discharge in the model shall be

A stone weights 450 N in air and 250 N in water. The volume of the stone is:

A beam is built using M25 concrete and Fe-250 bars of 16 mm dia bars. In limit state design, the development length, L_d, in terms of diameter of reinforcement, for compression zone is _______ mm.

[τbd = 1.4 N/mm²]

The system of equations x - 4y + 7z = 12 , 3x + 8y - 2z = 10, 26 z - 8y = 6

A steel bar of 20 mm Fe415 grade is embedded in a concrete block of M20 grade. The bond stress τbd = 1.2 MPa as per IS : 456-2000, for mild steel in tension. The length of embedment is 1m. The maximum pulling force that can be applied on the bar is ___________ kN

A single-stage impulse turbine with a diameter of 120 cm runs at 3000 rpm. If the blade speed ratio is 0.42, then, the inlet velocity of steam will be

A penstock is 3000 meters long. Pressure wave travels in it with a velocity of 1500 m/s. If the turbine gates are closed uniformly and completely in a period of 4.5 seconds, then it is called

Choose the correct statement(s) with respect to the Lag distance in computing the absolute minimum sight distance of the vehicle.

i. The reaction time is taken as 0.15sec

ii. The distance is dependent only on the coefficient of friction, reaction time and gradient

iii. It is depended on reaction time and velocity.

iv. The reaction time is the time required to observe the obstruction.

Considering two vehicles moving at a speed of 85kmph and 60 kmph on a road surface with skid resistance of 0.72 and braking efficiency of 55%, what will be the non-passing sight distance? Assume necessary data.

length of runway under standard condition is 1800m. the airport site has an elevation of 300m. it has reference temperature of 33°C. if the runway is to be constructed with effective gradient of 0.6%. then determine the corrected runway length

A vehicle moving at 40 kmph speed was stopped by applying the brake and the length of skidmark was 18 m. If the average skid resistance of the pavement is known to be 0.70, the brake efficiency of the the test vehicle (in %) is

A rectangular cross-section as shown below, experiences a maximum bending stress of 30 N/mm². The magnitude of force experienced by the shaded region is _____ kN.

Flexibility matrix of the beam shown below is If the support B settles by Δ/EI units, what is the reaction at B?

The stiffness matrix of a beam element is given as . Then the flexibility matrix is

What are the critical activities in the project network shown below. (Use PERT analysis)

A rectangular concrete beam of width 150 mm and depth 250 mm is prestressed by pretensioning to a force of 200 kN at an eccentricity of 30 mm. the cross-sectional area of the prestressing steel is 200 mm2. Take modulus of elasticity of steel and concrete as 2.1 x 105 MPa and 3 x 104 MPa respectively. The percentage loss of stress in the prestressing steel due to elastic deformation of concrete is ________.

A concrete beam prestressed with a parabolic tendon is shown in the sketch. The eccentricity of the tendon is measured from the centroid of the cross-section. The applied prestressing force at service is 1620KN. The uniformly distributed load of 45 KN/m includes self-weight.

The stress (in N/mm²) in the bottom fibre at Mid Span is

A thick cylinder of internal diameter 10 cm is subjected to an internal pressure of 50 N/mm², then the thickness of the cylinder according to the maximum shear stress theory, if yield stress is 270 N/mm² and factor of safety is 2, is _______mm

Calculate the standard error of the volume of a cuboid whose sides are A, B, and C have values given below and standard error as +/-___________ in cm³

A = 50.0 cm +/-.04 cm

B = 40.0 cm +/-.03 cm

C = 30.0 cm + /-.02 cm

A water mains 140 cm inner diameter contains water at a pressure head of 200 m. The minimum thickness of the metal shell required for the water mains, given that maximum permissible stress in the metal is 400 kg/cm², will be ___ mm.

FEM for the given beam is:

A 50 cm diameter pipe carries water (v = 0.294 × 10^–6 m²/s) at an average velocity of 10 m/s . The roughness of pipe surface is 0.8 mm. For fully rough turbulent flow, What is the boundary shear stress.

Determine the distance from the pipe wall at which local velocity is equal to the average velocity for turbulent flow in pipe

A water supply system is designed for a town with population of 2,50,000. Determine the fire demand (in ml/min) using empirical relationship and the Match List I and List II

Determine the critical deficit (in ppm) of dissolved oxygen when the stream flowing at a rate of 210 cumec with saturated dissolved oxygen limit of 10.6ppm is diluted with a sewage flowing at the rate of 1.35 cumec. Assume the Dissolved oxygen limit of waste water as 4ppm.

Which of the following are correctly matched:

1. Turbulent flow = Moment Integral equation

2. Laminar flow = Hagen Poiseuille equation

12m³/s of water is applied to a field having area of 30 hectares for 4 hours. About 0.3m of water stored in the root zone. Water application efficiency(%)in this case would be;

A body was subjected to two mutually perpendicular stresses of -6MPa and 24MPa respectively. What is the shear stress on the plane of pure shear?

The figure shows reducing area conduit carrying water. The pressure p and velocity V are uniform across sections 1 and The density of water is 1000 kg/m³. If the total loss of head due to friction is just equal to the loss of potential head between the inlet and the outlet, then V₂ in m/s will be _____

A job having a processing time of 11 days is to be processed in scheduling operation. The job is to be delivered on 18th july 2018 but the job is received on 7th july. Find the critical ratio of the job to be processed.

A rectangular beam of cross-section B × D has moment of resistance equal to M. A smaller square section is removed from the centre such that the moment of resistance of the remaining area is equal to half the initial MOR. The length of side of section removed is

During the construction of a highway bridge, the average permanent load on the clay layer is expected to increase by about 95 kN/m³. The average effective overburden pressure at the middle of the clay layer is 190 kN/m³. Here, H is 4.5 m, Compression index is 0.26, e₀ = 0.78, and coefficient of consolidation is 0.23 m²/month. The clay is normally consolidated. Determine the total primary consolidation settlement (in mm) and the ratio of pre-compression pressure to the effective stress of the bridge.