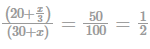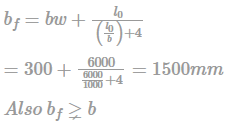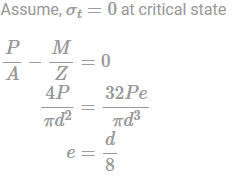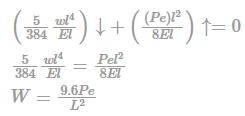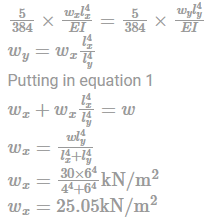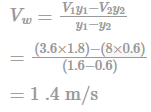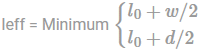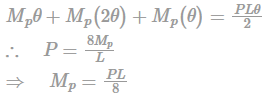Practice Test: Civil Engineering (CE)- 13
65 Questions MCQ Test GATE Civil Engineering (CE) 2023 Mock Test Series | Practice Test: Civil Engineering (CE)- 13
| 1 Crore+ students have signed up on EduRev. Have you? |
A monkey is trying to reach the top of a tree. He climbs 3 feet in a minute but slides down by 1.5 feet after each climb. If he reaches the top of the tree in 58 minutes, then the maximum possible height of the tree is ________ feets.
We can work out the maximum possible height of the tree as 1.5 x 57 + 3 = 85.5 + 3 = 88.5 feet
In the following question, a sentence has been given in Direct/Indirect Speech. Out of the four alternatives suggested, select the one which best expresses the same sentence in Indirect/Direct Speech.
My husband said to me, “Wait for me outside."
What of the following function(s) in an accurate description of the graph for the range(s) indicated?
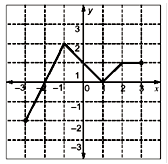
A. y = 2x + 4 for -3 ≤ x ≤ -1
B. y = |x-1| for -1 ≤ x ≤ 2
C. y = ||x|-1| for -1 ≤ x ≤ 2
D. y = 1 for 2 ≤ x ≤ 3
(i) y = 2x+4 is true in -3 ≤ x ≤ -1
On putting x = -3, y = 2 and x = -2,y = 0 and x = -1, y = 2
(ii) y = |x-1| is also true (x = -1, y = 2), (x = 0 ,y = 1) and (x = 1, y = 0)
(iv) y = 1 in (2 ≤ x ≤ 3) always true
(i), (ii) and (iv) are true.
A rectangular room having dimensions 3.74 m x 5.78 m is required to be tiled using a minimum number of identical square tiles. The number of such tiles and area of each tile (in cm2) is given by
In the following question, out of the four alternatives, select the alternative which best expresses the meaning of the Idiom/Phrase.
To take into account
In an examination, a candidate attempts all the questions since there is no negative marking and all the questions carry equal marks. Out of the first 30 questions that he attempts, he has marked correct options for 20 questions whereas out of the remaining questions, he is able to mark only one third question with correct option. His overall score in the examination is 50%.
The total number of questions in the paper are;
We can form equations based on the given information. Let ‘x’ be the number of questions attempted by him in the second part.
Or 40+ 2x/3 = 30 + x which leads us to get x/3 = 10 or x = 30
The total number of questions in the examination are x + 30 = 60
Amol, Brijendra, Chander and Dron are sitting around a roundtable. One of them is an electronics engineer (ECE) who is sitting to the left of the Mechanical Engineer (ME). Amol is sitting opposite a Computer Science Engineer (CSE). It is also known that Dron likes to play computer games and Brijendra is sitting to the right of Civil Engineer (CE). Identify the correct match from the given choices.
Based on the given data, we can say that Amol (ME) is sitting opposite to CSE – Brijendra. Civil Engineer has to be to the right of Amol – Mechanical Engineer. However, it is not possible to say whether Chander is an Electronics Engineer or a Civil Engineer AND likewise for Dron.
In five cities A is more populated than B which is less populated then E. D is more populated than E but not as populated as A. C is less populated than B. Which city has the highest population?
From first statement
A > B and B < E
From second statement
D > E and D < A
From third statement
C < B
From all statements together
A > D > E > B > C
One-third of Ramesh’s marks in Arithmetic is equal to half his marks in English. If he gets 150 marks in the two subjects to gather, how many marks has he got in English?
Let marks obtained by Ramesh in Arithmetic be ‘A’ and marks obtained in English be E.
As the information given,
1/3 A = E/2
à (A/3) – (E/2) = 0
à 2A – 3E= 0 ……….(i)
A + E = 150 …………(ii)
From equation (i) and (ii), E = 60
Hence, Ramesh got 60 marks in English.
In a test given by Prof Virus during the minors, Raju gets 32% marks and fails by 20 marks whereas Chatur gets 30 marks more than passing marks while scoring 42% marks. The marks required to get twice the passing marks are _______.
The difference in percentage marks obtained by Raju and Chatur is 42 – 32 = 10% whereas the difference in their marks is 20 + 30 = 50 (Raju gets 20 marks less while Chatur gets 30 marks more than pass marks).
This gives us 1% = 5 marks and the passing marks as 20 + 32% = 180.
The required marks = 360 (twice the passing marks)
During the subsurface investigations for design of foundations, a standard penetration test was conducted at 4.5m below the ground surface. The record of number of blows is given below.
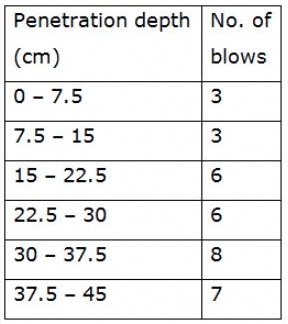
Q. Assuming the water table at ground level, soil as fine sand and correction factor for overburden as 1.0, the corrected ‘N’ value for the soil would be
So, here N = 6 + 6 + 8 + 7 = 27
Now, here N > 15 and water table at ground level so dilatancy correction is applied.
Ncorrected = 15 + 1/2(N−15)
= 15 + 1/2(27 - 15) = 21
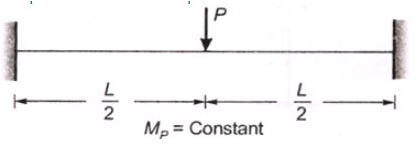
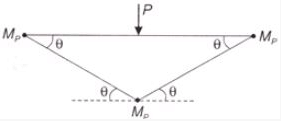
A beam-column having overall depth and width is 550 mm and 250 mm. If torsional moment for this beam is 30 kN.m then twisting moment will be-
& T = 30 kN .m
So, the twisting moment
MT = T (1 + D/b) / 1.7
= 30 (1 + 550/250) / 1.7
= 56.47 kN .m
An isolated ‘T’ beam is used on the walkway. The beam is simply supported with an effective span of 6 m. Effective width of flange for shown figure is :
Hence bf = 1000 mm
What is the maximum possible eccentricity in a prestressed concrete beam of circular cross-section? Diameter of the section is d. Tension is not allowed anywhere and any time in the cross-section. Neglect dead load (self-weight).
Deposit with flocculated structure is formed when
The process by which individual particles of clay aggregate into coltlike masses or precipitate into small lumps. Flocculation occurs as a result of a chemical reaction between the clay particles and another substance, usually salt water.
In the case of flocculated structure, there will be edge to edge and edge to face contact between the particles. This type of formation is due to the net electrical forces between the adjacent particles at the time of deposition being attractive in nature.
The concentration of dissolved minerals in water leads to formation of flocculated structures with very high void ratio as in the case of marine deposits.
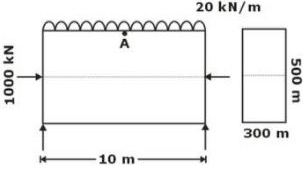
A simply supported prestressed beam of 300 × 500 mm in c/s is subjected to a superimposed load of 20 kN/m over a span of 10m. If a prestressing force of 1000 kN is applied through a straight tendon located along centroidal axis then what is the extreme top fiber stress at the mid section:
What will be the maximum possible uniformly distributed load (inclusive of self-weight) over the entire span of a simply supported beam of span ‘L’ such that the deflection at midspan at service condition is zero? The cross-section is rectangular. The prestressing force ‘P’ is applied with uniform eccentricity ‘e’. Assume no losses.
[δ due to self (weight + udl)] + [δ due to eccentric force P on cable] = 0
If Qs4 and Qs6 are the equilibrium discharges of S- curve for the catchment obtained by 4 hour UH summation and 6 hour UH summation, respectively, then Qs4/Qs6 is __________. (Up to 2 decimal places)
Qe = A.1D
Qs4/Qs6 = 6/4 = 1.50
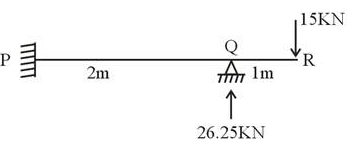
The beam PQR shown in the given figure is horizontal. The distance to the point of contraflexure from the fixed end P is _____m. (up to two decimal place)
15x = 26.25(x−1)
x = 2.334m
→ Distance from fixed end = 3 - 2.334 = 00.666m.
30 KN/m2 load acting on a 4m × 6m 2-way slab. Effective Load acting in a shorter direction is_____ KN/m2.
wy = Load acting in shorter direction
wx + wy = w
Equating deflection of both strips.
A stream function is given by:
Ψ = 3xy2 + (x2+2)y
The flow rate across a line joining points A(0,5) and B(1,2) is
ΨB = (3×1×22) + ((12 + 2) × 2) = 18
Flow rate across a line joining points A and B is
= ΨB − ΨA
= 18 − 10
= 8 units.
Before passage of a surge, the depth and velocity of flow at a section are 1.8 m and 3.6 m/s. After the surge passage, they are 0.6 m and 8 m/s respectively. The speed of the surge is?
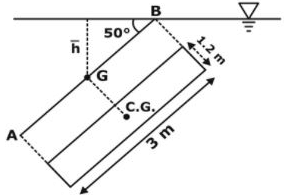
A rectangular plate 1.2 x 3 m is immersed in a liquid of relative density 0.85 with its 1.2 m side horizontal and just at the water surface. If the plane of plate makes an angle of 50o with the horizontal, the pressure force on one side of the plate is
Density of liquid = 0.85 x 1000 = 850 kg/m3
h = 1.5 sin 50o = 1.149 m
Pressure force on one side of plate = ρgAh = 850 x 9.81 x (1.2 x 3) x 1.149 = 34.5 kN.
A beam with both continuous ends has a clear span of 6m and supports 600 mm wide. The effective depth of the beam is 550 mm. As per IS 456-2000, the effective span of the beam (in m) is____________
i) When width of support < 1/12="" of="" clear="" />
ii) when width of support > 1/12 of clear span
a) When one end is fixed & other end continuous or both ends continuous.
leff = lo
b) When one end is continuous & the other end is simply supported.
As per given data, width of support = 600 mm & 1/12 of clear span = 500 mm
Hence leff = lo = 6m [since both ends are continuous]
A turbine develops 2516 kW at 240 rpm. The torque in the shaft is approximately:
Where, T = torque and N = speed in rpm
So, T = 60P/(2πN) = (60×2516×1000)/(2×3.14×240) = 100108Nm = 100kNm
A Kaplan turbine has a runner of diameter 4.0 m. The diameter of the hub is 1.6 m. If the velocity of flow and the swirl velocity at the inlet side of the blade at the hub are 6.0 m/s and 10.0 m/s, respectively, the flow and swirl velocities at the inlet side of the tip are, respectively:
The flow velocity remains the same throughout.
Hence Vf2 = Vf1 = 6 m/s
D1 = 1.6; D2 = 4; u2 = 10m/s
Hence u1 = 4 m/s
A pipe of 30 cm diameter conveying 300 l/s of water has a right-angled bend in a horizontal plane. The resultant force exerted on the bend if pressure at inlet and outlet of the bend are 24.525N/cm2 and 23.544N/cm2 is ___ N.
D = 30 cm
A1 = A2 = π/4D2 = 0.07068 m2
V = V1 = V2 = Q/A = 0.3/0.07068 = 4.244 m/s
Now, θ = 90°,
P1 = 24.525 N/cm2 = 24.525 × 104 N/m2
P2 = 23.544 × 104 N/m2
Force along x-axis on bend,
LFx = pQ[V1x - V2x]+(P1xA1) + P2xA2
Fx = 1000 × 0.3[4.244-0] + 24.525 × 104 × 0.07068 + 0
Fx = 18607.5N Similarly, force along y-axis on bend,
Fy = pQ [V1y - V2y] + P1yA1 + P2yA2
Fy = 1000 × 0.3 [0- 4.244 ] + 0 - 235440 × 0.07068
Fy = 17914.1 N
FR = 
A sample of saturated cohesionless soil tested in a drained triaxial compression test showed an angle of internal friction of 30°. The deviator stress at failure for the sample at a confining pressure of 200kPa is equal to
Where, α = 45 + ϕ/2
α = 45∘ + 30∘/2 = 60∘, σ1 = 3σ3 = 3 × 200 = 600 kPa
∴ Deviatoric stress = σ1 - σ3
= 600 - 200 = 400 kPα
The daily cover of MSW landfills consists of which one of the following?
Two different soil types (soil I and Soil 2) are used as backfill behind a retaining wall as shown in the figure, where gt is total unit weight, and c ¢ and f ¢ are effective cohesion and effective angle of shearing resistance. The resultant active earth force per unit length (in kN/m) acting on the wall is:
What is the final end moment in the following structure?
Moment at the joint,
= 35 cos 45 × 2 + 35 sin 45 × 4
= 148.5 kNm
Stiffness of AB = 4EI/6
Stiffness of BC = 3EI/6
Distribution factor of AB,
Moment transferred to AB,
MBA = (4/7) × 148.5 = 84.86 kNm
Fixed end moment
MAB = (1/2) × 84.86 = 42.43 kNm
In an irrigation project, in a certain year, 70% and 46% of the culturable command area in Kharif and Rabi, respectively, remained without water and the rest of the area got irrigation water. The intensity of irrigation in that year for the project was
= Intensity in Rabi + Intensity in Kharif
= (100-46) + (100-70)
= 84%
A retaining wall is constructed in a clayey soil. The height of the backfill is found to be 9m, the unit weight of the sand is 2t/m3 and the angle of internal friction is 30˚. Find out the earth pressure per meter length on the retaining wall with a smooth vertical back.
Active earth pressure per unit length = 0.5 x Kα x y x H2 = 0.5 x (1/3) x 2t x 9 x 9 = 27t/m
Activities A, B, C and D constitute a small project; their interrelationship, expected duration and standard deviation of this expected duration are shown in the figure, respectively.
With a view to improving the speed of implementation, each of B, C and D are split into three equal segments, maintaining appropriate inter-relationships between A and each of these nine segments. What will be the standard deviation of the modified project duration after segmentation (to the nearest 1/10in unit)?
If activity B is divided into 3 equal parts then each part will have duration 3 units and standard deviationσ1
= 5.6
The infiltration capacity of a soil follows the Horton's exponential model, f = c. During and experiment, the initial infiltration capacity was observed to be 200 mm/h. After a long time, the infiltration capacity was reduced to 25 mm/h. If the infiltration capacity after 1 hour was 90 mm/h, the value of the decay rate constant, k (in 11', up to two decimal places) is____
Horton's infiltration capacity
f = fc + (f0−fi)e−∞t
fε = ultimate infiltration capacity = 25 mm/hr
f = Initial infiltration capacity = 200 mm/hr
f = Infiltration capacity = 90 mm/hr
f = fc + (f0−fi)e−∞t
90 = 25 + (200 - 25) e-∞x1
175e-x = 65
E-x = 0.371
∝ = 0.9915; ∝ = 0.99/hou!
Reciprocal leveling was done between two points A and B, the readings of which are as shown below, which are 700 mm apart.
If the atmospheric conditions do not change during the period of observation and R.L. of A is 126.49 m, then the R.L. of B is _______ m.
True difference of level between A and B
hb = reading on staff at B when instrument at A = 1.64
ha = reading on staff at A when instrument at A = 1.05
hb = reading on staff at B when instrument at B = 1.53
ha = reading on staff at A when instrument at B = 0.90
⇒ H = 0.61m ∴ R.L. of B = R.L. of A-H = 125.88m
Note: R.L of B
Let P be a 2 ×2 real orthogonal matrix and 
is a real vector [x1, x2]T with length 
Then, which one of the following statements is correct?
P be a 2×2 real orthogonal matrix
= [x1 x2] be a real vector
Magnitude or length
For orthogonal matrix P,
PPT = PTP = 1
P2 × 2 & 
2x1
hence,
where C is the curve x2 + y2 = 4
(Using green theorem)
= 0
Determine the specific gravity of the liquid Y for the fig. given below.
Given: SX = 1.3 pa = 24 k N/m2
As liquid has been moved towards A which means Pa will be vacuum pressure
pa = -24 kN/m2 Pressure at pt. P,
pP = -24 + (1.3 × 9.81 × 0.8) = -13.8 kN/m2 Air column is present between points P & Q;
Therefore pP = pQ
Also pt. S is at atm. Pressure, pS = 0 = pR
The specific gravity of liquid Y,
pS = pQ + (SY × 9.81 × 1)0
= -13.8 + (SY × 9.81 × 1) SY
= 1.406
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.
[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]
Stopping sight distance = 200 m
∴ The length of summit vertical curve is given by
= 389.69 m >200 m (O.K)
The variance of the random variable X with probability density function f(x) = 1/2 |x|e-|x| is ___________.
Given, f(x) = 1/2 |x|e-|x|
By definition, variance is
dx since it is an odd function, we get
Hence,
V(x) = 6 - (0)2
= 6.
Let X and Y be independent random variables. Given that X has a uniform distribution over –1 ≤ x ≤ 1 and ▁Y = 2 and ▁(Y^2 )=6 Another random process W(t) is defined as W(t) = (Y + 3Xt) ⋅t
The mean square value of W(t) is
Given, W(t) = (Y+3Xt).tE[W2(t)] = E[Y2 + 9 × 2t2 + 6 × Yt]t2 = E[Y2t2] + E[9 × 2t4] + E[XYt3] ∵ Y2 = 6 and X Y are independent
fx(X) = ∫1-1adx = 1
The state of the soil when plants fail to extract sufficient water for their requirements is _____.
Permanent wilting point is defined as when a plant fails to extract sufficient water to grow crops. And finally the plant wilt up.
The maximum shear stress in a rectangular beam is_____ times of average shear stress
For Rectangular Sections.
For a rectangular section at any distance y from the Neutral Axis:
Substituting in equation
This shows that there is a parabolic variation of Shear Stress with y. The maximum Shear Force occurs at the Neutral Axis and is given by:
s = 2F/2bd
If F/bd is called the Mean Stress then:
s = 1.5 × smean
The laboratory tests on a soil sample gave the following results:
1). Natural water content, wn = 25%
2). Liquid limit, wL = 60%
3). Plastic limit, wp = 35%
4). Percentage of particle less than 2μ = 20%
Q. The value of activity number is
Plasticity index,
Ip = WL-WP = 60-35 = 25%
Soil activity (A) is a number equal to IP/CF, where IP is the plasticity index of soil, and the CF is percentage of clay particles in soil (particles smaller than 2 microns)
Activity number
IP/c = 0.25/0.20 = 1.25
An average data for conventional activated sludge treatment plant is as follows:
Wastewater flow = 35000 m3/d
Volume of aeration tank = 10500 m3
Influent BOD = 230 mg/L
Effluent BOD = 20 mg/L
Mixed Liquor suspended solids (MLSS) = 2200 mg/L
Effluent suspended solids = 30 mg/L
Waste sludge suspended solids = 9500 mg/L
Quantity of waste sludge = 200 m3/day
Assume MLVSS = 75% MLSS
Based on the above information, the oxygen requirement of the aeration tank is _________ tonnes/day.
Given, V = 10500 m3, X = 2200 mg/L
Qo = 35000 m3/d; Qw = 200 m3/d
Xu = 9500 mg/L; Xe = 30 mg/L
O2 required = 8110823.53 gm/day
O2 required = 8.11 tonnes/day
The Atterberg limits of a soil are LL = 68% and PL = 34% and it contains 85% by weight of clay. The water content of a sample is 45%. Determine the predominant clay mineral.
Plasticity index IP = LL – PL = 68 − 34 = 34
Liquidity index IL = (w-PL)/IP = (45-34)/34 = 0.32
Activity, A = IP/%clay particles = 3485 = 0.40
The clay is likely to be predominantly kaolinite.
A rectangular column section of 250mm x 400mm is reinforced with five steel bars of grade Fe 500, each of 20mm diameters. Concrete mix is M30. Axial load on the column section with minimum eccentricity as per IS: 456-2000 using limit state method can be applied upto
A = 250 × 400 = 105 mm2
ASC = 5 × π/4(20)2 = 1570.8mm2
Ac = A−As = 98429.2mm2
Axial load, Pn = 0.4fckAc + 0.67 fy . Asc
= 0.4 × 30 × 98429.2 + 0.67 × 500 × 1570.8
= 1707.37 kN
A prestressed concrete beam (pretensioned) has the following cross-section as shown in figure below. Initial prestress = 1200 N/mm2 (in both wires).
Young’s modulus of steel, ES = 210 × 103 N/mm2, Young’s modulus of concrete, EC = 36 × 103 N/mm2
What will be the loss of pre-stress (in N/mm2) in top steel wires due to elastic shortening?
[Assume moment of Inertia about centroid axis = 8575 × 106 mm4]
Resultant prestressing force
where, PR = Pt + PB ...(i)
Force in upper tensioned steel,
Pt = 16 × π/4 × 52 × 1200
= 376991 N = 376.991 kN
Force in bottom tensioned steel,
Ps = 30 × π/4 × 62 ×1200
= 1017876 N = 1017.876 kN
PR = 376991 + 1017876
= 1394867 N
Depth of centroidal axis from top,
Eccentricity of resultant force from the centre of beam section,
eR = 436.76 — 350 = 86.76 mm
Stress in concrete at the level of top steel,
loss of stress in top steel m.fc.top
= × 2.41 = 14.06N/mm2
A 60 mm-diameter water jet strikes a plate containing a hole of 40 mm diameter as shown in the figure. Part of the jet passes through the hole horizontally, and the remaining is deflected vertically. The density of water is 1000 kg/m3. If velocities are as indicated in the figure, the magnitude of horizontal force (in N) required to hold the plate is ______.
= (P1-Pt)x-direction
= m1V1-m2V2)x-direction
= VpA1V1 - pA2V2 (∴V1 = V2)
= pV2(A1-A2)
= 100 × 20 × 20 × π/4[0.06)2 - (0.04)2
= 628.32N
For a fluid the apparent viscosity is varying with rate of shear strain a shown in the following table
Q. What type of fluid is
As the rate of deformation increases, the apparent viscosity decreases. The behaviour of fluid is known as shear thinning which is also known as pseudoplastic fluid.
Maximum strain theory for the failure of a material at the elastic limit is known as
St. Venant's theory is also known as maximum principal strain theory.
According to this theory, material subjected to complex stresses fails in simple tensile tests, when maximum principal strain reaches the value of strain at yield point.
For three soil layers A, B and C of cross-section 100mm x 100mm each shown, the permeability is 1.1 x 10-2 cm/sec, 2.9 x 10-3 cm/sec and 4.2 x 10-4 cm/sec respectively. The rate of water flow (in cm3/sec ) is
Though it looks like horizontal flow, in actual condition it is vertical flow of water as there is no cross-section through each layer. Therefore, every layer has same flow q = q1 = q2 = q3 and the total head is ∆h = ∆h1 + ∆h2 + ∆h3
Flow through soil, q = kv(eqv) ∆h/L A = 1.065 × 10-3cm/sec × 300/450 × (10cm × 10cm)
q = 0.071cm3/sec
It required a time of 3 min 30 sec for 40% consolidation of a 35-mm-thick clay layer (2- way drainage condition) in the laboratory. How long (in days) will it take for a 4-m-thick clay layer of the same clay in the field under the same pressure increment to reach 40% consolidation? In the site, there is a rock layer at the bottom of the clay.
12000 × 16 = tfield
⟹ 192000 sec = 133 days
A sheet piling system with its corresponding flow net is shown in figure. Take and hydraulic conductivity as 2 x 10-5 cm/s. Estimate (a) rate flow in cm3/s (b) For the element A with l= 1.2m, calculate the average velocity.
∆H =10 m
Here Nd= 14, Nf= 4
(a) q = k ∆H Nf/Nd
On substituting, flow rate, q = 2 x 10-5 x 10 x 102 x 4/14
q = 7.14 x 10-3 cm3/s = 0.0071 cm3/s
(b) velocity , v = ki
i = ∆H/L
i = 10/1.2 = 8.33
v = 2 x 10-5 x 8.33 = 1.67 x 10-4 cm/s = 0.00017 cm/s
A reservoir of surface area 400 hectares has water temperature = 27°C, relative humidity = 40%, ea of water = 17.54 mm (Hg) and velocity of wind 2 m above the ground is 11 km/hr. Use Meyer’s formula to determine the daily evaporation from the reservoir in mm.
E = Km(es – ea) (1 + v9/16
Km = 0.36
Relative humidity, ea/es = 0.4
es = 17.54/0.4 = 43.85 mm of Hg
Velocity of wind at 9 m above ground, v9/v2 = (9/2)1/7
v9 = 11 × 1.239 = 13.629 km/hr
Putting in Meyer’s Formula, E = 0.36(43.85 – 17.54) (1 + 13.629/16) = 17.539 mm/day
The following figure shows the velocity-time plot for a particle travelling along a straight line. The distance covered by the particle from t=0 to t=5s is ______ m.
Distance covered=Area under the curve between t = 0s to t = 5s
= 1/2 × 1 × 1 + 1 × 1 + 1/2 × (1 + 4) × (3 - 2) + 1/2 × (4 + 2) × (5-3)
= 0.5 + 1 + 2.5 + 6 = 10
A bracket connection is formed as shown in figure using 4 bolts of 20 mm dia and grade 4.6. The service load P (in kN) that can be carried by the connection is
[Use LSM and assume failure to be critical in shear and failure shear plane lies in threaded portion of bolt]
Strength of bolt in single shear,
For safety, F ≤ Vsb
0.9P1 = 45.27
P1 = 50.30 kN
Service load,
P = P1/Load factor = 50.3/1.5 = 33.53 kN
In a pair of overlapping photographs, the mean distance between two principal points both of which lie on the datum is 6.375 cm. At the time of photography, the aircraft was 600 m above the datum. The camera has a focal length of 150 mm. in the common overlap a tall chimney 120 m high with its base in the datum surface is observed. Determine the difference of parallax for top and bottom of chimney.
Scale of the photograph for datum elevation,
S = f/H = (150/1000)/600
= 1/4000
For the datum elevation,
B/b = H/f
Or B = H/f . b
= 4000×6.375/100 = 255 m
The parallax for the top and bottom of the chimney are calculated from the equation
P = Bf / (H-h)
For bottom of chimney, h = 0
Hence p1 = 255×150/600 = 63.75 mm
For the top of chimney, h = 120 m
Hence p2 = 255×150 / (600-120)
= 79.69 mm
Difference of parallax is given by,
Δp = p2 – p1
= 79.69 – 63.75 = 15.94 mm.
Solution of dy/dx = y2 × x3 at x = √5 and y = 2 is
dy/dx = y2 × x3
⇒ dyy2 = x3dx
Integrating both sides.
The value of integral 
exdx calculated using simpson's 1/3rd Rule, with 10 subintervals is use the table given
y2 + y2 + y6 +...+ yn]
= 1/3 × 0.1[y0 + 4y1 + y3+ y5 + y7 + y9 +2
y2 + y4 + y6 + y8 + y10]
= 1/3 × 0.1[2.718+4(3.004+3.669+4.482
+5.474+6.686)+23.320+4.055+4.953+6.050+7.389]
0.1/3[2.718+423.315+218.378+7.389)
= 0.1/3[140.1232]
exdx = 4.67077
In the following table, x is a discrete random variable and p(x) is the probability density. The difference between the variance & the standard deviation is
+4×0.1×5×0.15+6×0.15
= 0.2+0.5+0.45+0.4+0.75+0.9 = 3.2
Ex2 = ∑ixi2pi = (1)2 × 0.2+(2)2×0.25
+(3)2×0.15+(4)2×0.1
+(5)2×0.15+(6)2×0.15
=1×0.2+4×0.25+9×0.15
+16×0.1+25×0.15+36×0.15
= 0.2+1+1.35+1.6+3.75+5.4=13.3
= Ex2-Ex2
Variance = 13.3-(3.2)2=13.3-10.24=3.06
Standard Deviation σ= 
= 
= 1.749
Difference of variance & standard deviation = 3.06 – 1.749 = 1.311
A fair coin is tossed independently five times. The probability of the event "the number of times tails show up is less than the number of times heads show up” is
Coin is tossed 5 times
P(number of tails < number="" of="" />
= p5x & oT or 4x & IT or 3x & 2T
= p(exactly 5 neads) + p(exactly 4 heads)
+ p(exactly 3 heads)
Consider the following equations
3x – y – z + 2w = 0
3x + y – z - 2w = 0
12x + 3y – 4z - 6w = 0
The system of equations will be
The above system of equations can be written as AX = B.
∴ Rank (A) = Rank 2 and number of variables = 4
∴ The system is consistent having many solutions.
|
27 docs|296 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
27 docs|296 tests
|
Download free EduRev App
Related content with Practice Test: Civil Engineering (CE)- 13
|
|
|
|
Related tests with Practice Test: Civil Engineering (CE)- 13
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
