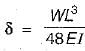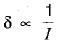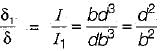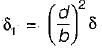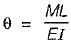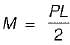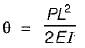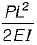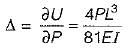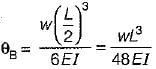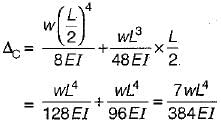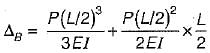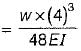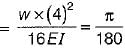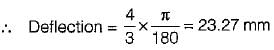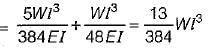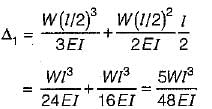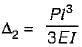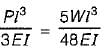Test: Deflection of Beams - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2026 Mock Test Series - Test: Deflection of Beams - 1
A simply supported beam with width ‘b' and depth ‘d’ carries a central load W and undergoes deflection δ at the centre. If the width and depth are interchanged, the deflection at the centre of the beam would attain the value
Two identical cantileversare loaded as shown in figure. If slope at the free end of the cantilever in figure (a) is θ, the slope at the free end of the cantilever in figure (b) will be.


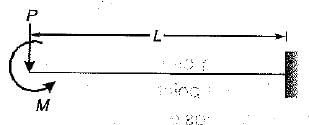
The given figure shows a cantilever of span L subjected to a concentrated load P and moment M at the free end. Deflection at the free end is given by

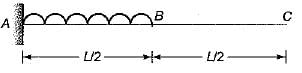
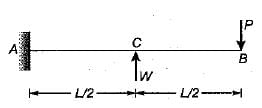
An overhang beam of uniform El is loaded as shown

The deflection at the free end will be
A horizontal beam of length l of uniform cross-section is pinned at ends A and B. At end A there is an anticlockwise moment M and at end B there is clockwise moment 2M. The slope at end A and end B are respectively.
A cantilever beam of length ‘l’ carries a UDL ‘w’ from fixed end till mid span. The deflection at the free end is given by
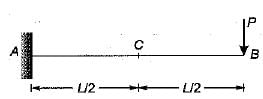
A cantilever beam of length ’L’ is subjected to a concentrated load P at free end what is the deflection at the centre of beam?
A 4-metre long beam, simply supported at its ends; carries a point load 'W at its centre. If the slope at the ends of beam is 1° then deflection at the centre of beam is
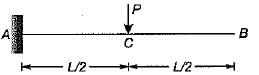
A simply supported beam AB of span ‘l’ has a uniform cross-section throughout. It carries a central concentrated load W and another load which is uniformly distributed over the entire span, its total magnitude being W. The maximum deflection in the beam is
A cantilever beam of span ‘l’ and uniform flexural rigidity ‘EI’ is loaded with an upward force ‘W’ at the mid point and downward force ‘P’ at the free end. The deflection at the free end will be zero if
|
33 docs|291 tests
|