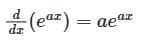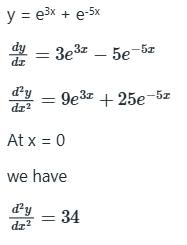Test: Differential Equations & Multiple Integrals- 2 - Mechanical Engineering MCQ
30 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Test: Differential Equations & Multiple Integrals- 2
The volume of an object expressed in spherical co-ordinates is given by
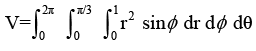
The value of the integral is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
By a change of variable x (u, y) = uv, y (u, v) = v/u is double integral, the integrand f(x, y) changes to f(uv, v/u) φ (u,v). Then, φ (u, v) is
Consider the shaded triangular region P shown in the figure. What is
A path AB in the form of one quarter of a circle of unit radius is shown in the figure. Integration of (x + y)2 on path AB traversed in a counterclockwise sense is
A parabolic cable is held between two supports at the same level. The horizontal span between the supports is L. The sag at the mid-span is h. The equation of the parabola is where x is the horizontal coordinate and y is the vertical coordinate with the origin at the centre of the cable. The expression for the total length of the cable is
A surface S(x,y)=2x+5y-3 is integrated once over a path consisting of the points that satisfy ( x +1)2+ (y − 1)2 = √2 . The integral evaluates to
The order of the differential equation
The solution of the differential equation under the boundary conditions
(i) y =y1 At x = 0 and
(ii) y =y2 At x = ∞,
Where k, y1 and y2 are constants, is
A function n(x) satisfies the differential equation where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is
The solution of the differential equation
The solution to the differential equation f’’(x)+4f’(x)+4f(x)=0 is
Which of the following is a solution of the differential equation
The degree of the differential equation
The solution for the differential equation with the condition that y = 1 at x = 0 is
A spherical naphthalene ball exposed to the atmosphere loses volume at a rate proportional to its instantaneous surface area due to evaporation. If the initial diameter of the ball is 2 cm and the diameter reduces to 1 cm after 3 months, the ball completely evaporates in
Solution of the differential equation represents a family of
A body originally at 60ºC cools down to 40ºC in 15 minutes when kept in air at a temperature of 25ºC. What will be the temperature of the body at the end of 30 minutes?
The partial differential equation that can be formed from z = ax + by + ab has the form
With K as constant, the possible solution for the first order differential equation is
The boundary-value problem yn + λy = 0, y(0) = y(λ) = 0 will have non-zero solutions if and only if the values of λ are
The solution of the differential equation with the condition that y = 1 at x = 1, is
Consider the differential equation 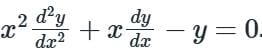 Which of the following is a solution to this differential equation for x > 0?
Which of the following is a solution to this differential equation for x > 0?
If y = e3x + e-5x find the value of
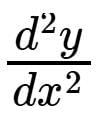 at x = 0
at x = 0
|
29 docs|220 tests
|
|
29 docs|220 tests
|