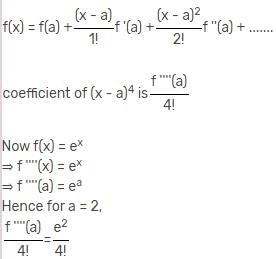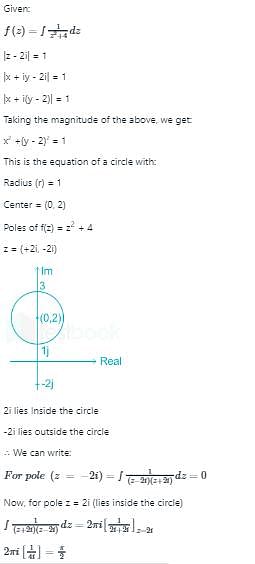Test: Fourier Series, Numerical Methods & Complex Variables- 1
20 Questions MCQ Test GATE Mechanical (ME) 2023 Mock Test Series | Test: Fourier Series, Numerical Methods & Complex Variables- 1
| 1 Crore+ students have signed up on EduRev. Have you? |
The Fourier series of a real periodic function has only
P. cosine terms if it is even
Q. sine terms if it is even
R. cosine terms if it is odd
S. sine terms if it is odd
Which of the above statements are correct?
Because sine function is odd and cosine is even function.
For the function e–x, the linear approximation around x = 2 is
(neglecting higher power of x)
In the Taylor series expansion of exp(x) + sin(x) about the point x = π, the coefficient of (x – π)2 is
The function x(t) is shown in the figure. Even and odd parts of a unit-step function u(t) are respectively,
In the Taylor series expansion of ex about x = 2, the coefficient of (x - 2)4 is
Taylor series expansion of f(x) about a is given by
The Fourier series expansion of a symmetric and even function, f(x) where
Will be
f(x) is symmetric and even, it’s Fourier series contain only cosine term. Now.
The Fourier series expansion 
of the periodic signal shown below will contain the following nonzero terms
from the figure, we can say that f(t) is an symmetric and even function of t. as cost is even function so choice (b) is correct.
The Fourier series for the function f(x)=sin2x is
Here f(x ) = sin2 x is even function, hence f( x ) has no sine term.
X(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π (2k ) /T ; k = 1, 2,.... Also, no sine terms are present. Then x(t) satisfies the equation
No sine terms are present.
∴x(t ) is even function.
The residue of the function f(z) 
The residues of a complex function 
at its poles are
x(z) has simple poles at z = 0,1, 2.
The value of the contour integral 
in positive sense is
The integral 
evaluated around the unit circle on the complex plane for 
An analytic function of a complex variable z = x + iy is expressed as f(z) = u (x, y) + i v(x, y) where i =√−1 . If u = xy, the expression for v should be
Here u and v are analytic as f(z) is analytic.
∴ u, v satisfy Cauchy-Riemann equation.
The analytic function 
has singularities at
The value of the integral 
(where C is a closed curve given by |z| = 1) is
Roots of the algebraic equation x3 +x2 +x+ 1 = 0 are
The algebraic equation
F (s ) = s5 − 3s4+ 5s3− 7s2 + 4s + 20 is given F ( s ) = 0 has
we can solve it by making Routh Hurwitz array.
We can replace 1st element of s1 by 10.
If we observe the 1st column, sign is changing two times.
So we have two poles on right half side of imaginary
Axis and 5s2+20=0
So, s =±2j and1 pole on left side of imaginary axis .
The value of 
Where C |z - 2i| = 1 is will be
Concept:
Cauchy's Integral Formula
If f(z) is analytic within and on a closed curve and if a is any point within C, then:
∫Cf(z)z−adz=2πif(a)
Analysis:
Given:
f(z)=∫1z2+4dz
|z - 2i| = 1
|x + iy - 2i| = 1
|x + i(y - 2)| = 1
Taking the magnitude of the above, we get:
x2 +(y - 2)2 = 1
This is the equation of a circle with:
Radius (r) = 1
Center = (0, 2)
Poles of f(z) = z2 + 4
z = (+2i, -2i)
2i lies Inside the circle
-2i lies outside the circle
∴ We can write:
Forpole(z=−2i)=∫1(z−2i)(z+2i)dz=0
Now, for pole z = 2i (lies inside the circle)
∫1(z+2i)(z−2i)dz=2πi[12i+2i]z=2i
Let z3 = z, where z is a complex number not equal to zero. Then z is a solution of
Now by hit and trial method we see the solution being
Z4 = 1
|
27 docs|243 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
27 docs|243 tests
|
Download free EduRev App
Related content with Test: Fourier Series, Numerical Methods & Complex Variables- 1
|
|
Related tests with Test: Fourier Series, Numerical Methods & Complex Variables- 1
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
