Gate Practice Test: Electrical Engineering(EE)- 13 - Electrical Engineering (EE) MCQ
30 Questions MCQ Test - Gate Practice Test: Electrical Engineering(EE)- 13
There are two lines made by joining points A, B, C. B lies between the line joining A and C. Is the distance between the A and C passes through the B more then 7 Km.
I. The distance between A and B is 6 Km
II. Distance between B to C is 7 Km long,
Comprehension:
Direction: In the given question, a word/phrase is given followed by three statements; I, II and III. Choose the pair of sentences which can be combined using the given word/ phrase when used at the beginning of the new sentence.
And
I: When Lionel Messi, Ronaldo and Neymar kick and dribble the football, they don’t remain confined to Argentina, Portugal or Brazil, respectively.
II: Let the entire world realise that through sports, especially football, we all can cement our bonds, wash away our bitterness and prejudices.
III: Live with a greater sense of closeness and joy with each other.
Which of the following is the MOST SIMILAR in meaning to Accreditation?
In how many ways can you place 2 white bishops on an empty chess board?
Comprehension:
Direction: In the question below are given statements followed by some conclusions. You have to take the given statements to be true even if they seem to be at variance with commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts.
Question:
Statement:
No physics is maths.
Some chemistry is maths.
All sciences are chemistry.
Conclusion:
I. No science is physics.
II. Some physics are science.
III. Some physics are chemistry.
Comprehension:
Direction: Read the information carefully and give the answer of the following questions-
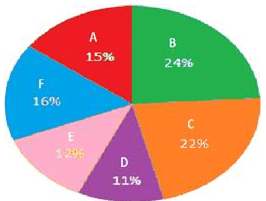
(This pie chart shows the percentage of students appear in six different exams in 2016)
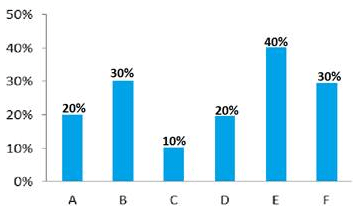
Question:
This bar graph shows the percentage of failed students which appear in these six different exams in 2016)
If in 2016, total number of failed students in exam F was 4080, then how many passed students appears in the exam B?
Comprehension:
Direction: Two sentences with two blanks in each, followed by five alternatives with two words in each, are given. Choose that option as the answer which can fill both the blanks of both the sentences.
Question:
i. A sinking feeling of panic ________ over them and a temporary paralyzing fear engulfed them ________.
ii. Being a cleanliness freak, she ________ the floor and went down to the market only after the house was _________ clean.
Comprehension:
Direction: Five statements are given below, labelled 1, 2, 3, 4 and 5 which are supposed to be in a logical order. A statement labelled P is given thereafter. P can replace one of the five statements such that the four statements along with P would make a coherent paragraph. You have to identify which statement should P replace and then the find out the correct sequence from the options. If the five options are in logical order and form a coherent paragraph/passage, choose the fifth option “12345”.
Question:
1) The future of Germany’s coalition government is hanging in the balance after the country’s interior minister reportedly announced his intention to resign over a migration showdown with Angela Merkel.
2) Horst Seehofer, who is also leader of the Christian Social Union, on Sunday night offered to step down from his ministerial role and party leadership in a closed-door meeting in which he and fellow CSU leaders had debated the merits of the migration deal Merkel hammered out with fellow European Union leaders in Brussels.
3) But with CSU hardliners believed to have tried to talk the combative interior minister into staying, a press conference was postponed until Monday, with Seehofer seeking to go back to Merkel in search of a final compromise.
4) At a 2am media conference, Seehofer said he had agreed to meet again with Merkel’s party before he made his decision final.
5) “We’ll have more talks today with the CDU in Berlin with the hope that we can come to an agreement,” Seehofer said.
P. Merkel said on Sunday she wanted the CDU and its Bavarian allies to continue working together.
4 identical solid spheres are melted and re-formed into a solid hemisphere. Then, the ratio of the curved surface area of the hemisphere to half of the surface area of a single sphere is -
A study of people who reduced the calories they consumed has found the strongest evidence yet that such restrictions slow down metabolism, raising hopes that a low calories lifestyle or treatments stimulating biological effects of restricted eating, could prolong health in old age. The report provides the most robust evidence to date that everything we have learnt in other animals can be applied to humans.
Which of the following argument will prove that the above conclusion is flawed?
A single core cable has a conductor diameter of 2 cm and an overall diameter of 4 cm. If the resistivity of the insulating material is 8×108 megohm-cm while the length of the cable is 2km then calculate the insulation resistance of this cable?
Which of the following conditions are correct for the convergence of the fourier transform of the function x(t).
1) x(t) is absolutely integrable over the range of time period.
2) x(t) should have finite number of discontinuities within any finite interval.
3) x(t) should have finite number of maxima and minima within any finite interval.
4) x(t) must be periodic.
Find the series equivalent inductance of the network that causes an opposite angle (Hays bridge) to null with the following bridge arms.
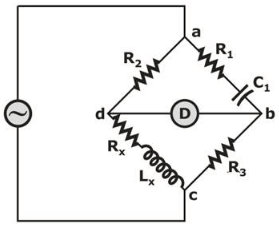
ω = 3000 rad/sec, R2 = 10 kΩ
R1 = 2 kΩ, C1 = 1 μF, R3 = 1 kΩ
The value of Lx in Henry will be
The Taylor series expansion of 3 sin x + 2 cos x is
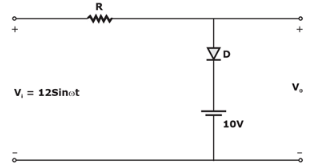
The above circuit shown above will behave as:
The loop transfer function of a system is given by ![]() The total number of root loci is:
The total number of root loci is:
Given below is arrangement of different counters the input frequency of clock is f0 and the output frequency is f0/n. The value of n will be

The no load voltage of a transformer is 440 V and its load current is 10 A. If the equivalent resistance & reactance are 0.12 Ω and 2.42 Ω and is operating at a power factor of 0.8 lagging, then find the % voltage regulation of the transformer.
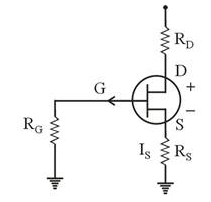
A p-channel JFET has VP=4V and IDSS=12mA. It is used in the circuit of figure given below with VDD=12V. Determine RD and RSso that ID=4mA and VDS = 6V
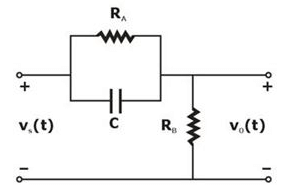
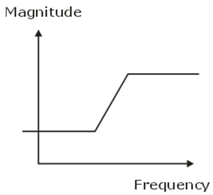
Which of the following plot represents the magnitude of transfer function versus frequency of the circuit shown in figure.
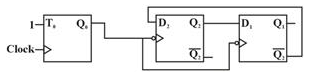
For the flip flop configuration as shown above for clock input to T flip flop. The mod of the above flip flop configuration will be _______.
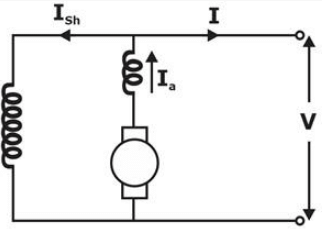
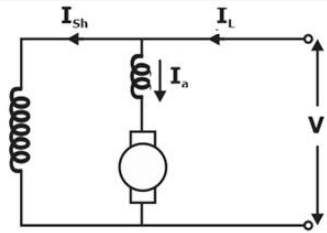
A compound DC generator is supplying a load and working as cumulative generator. If now machine behave as a motor, it will behave as:
Which one is increased when of negative feedback voltage is applied to an amplifier?
A circular disc of radius 5 m with a charge density of ρs = 12 sinϕ μC/m2 is enclosed by a surface S. The net flux crossing the S is.
For IOL (max) = 16mA, IIL(max) = 0.0016 A. The fan-out (low) will be
Two continuous time system is described as x1 (t)=te-t u(t) and x2 (t)=te-2t u(t), then the convolution of x1(t) & x2(t) will be?
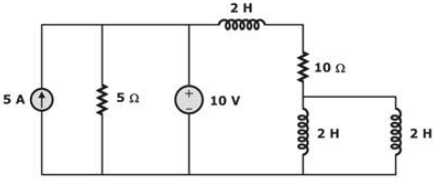
What will be the time constant of the given circuit:
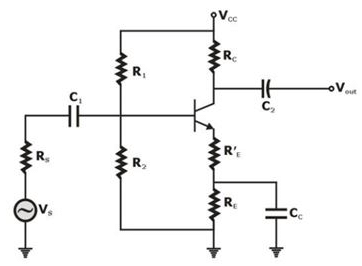
Which feedback topology is employed in the amplifier circuit below?
Boolean expression ![]() , its maxterm form is
, its maxterm form is
For a unity negative feedback system with the forward transfer function![]() Find the sum of maximum and minimum value of K to make the system stable.
Find the sum of maximum and minimum value of K to make the system stable.



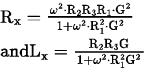
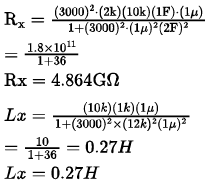
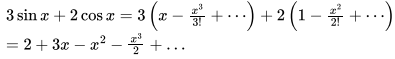
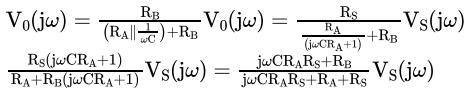
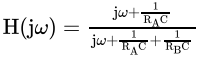
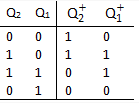
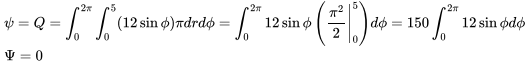
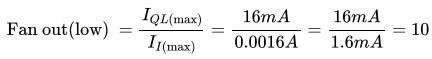
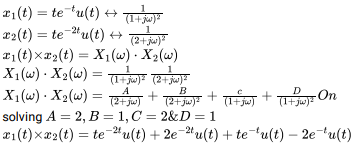
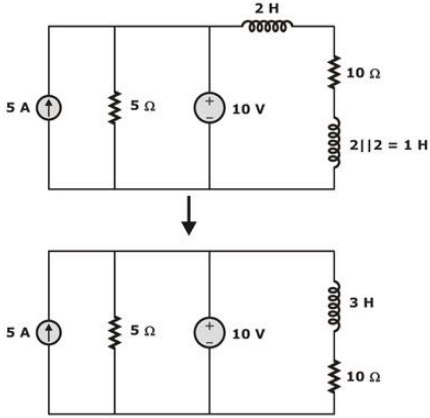
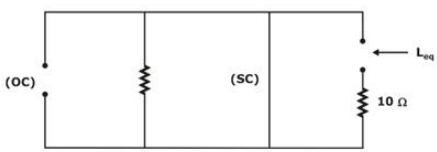
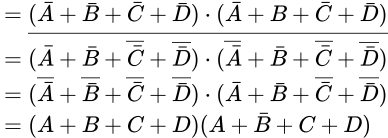
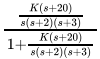 On simplifying we have
On simplifying we have











