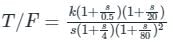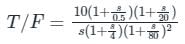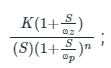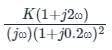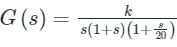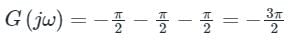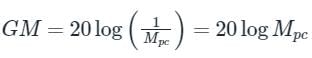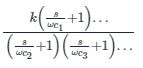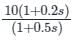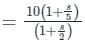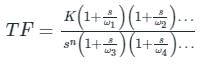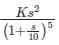Test: Bode Plot - 2 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: Bode Plot - 2
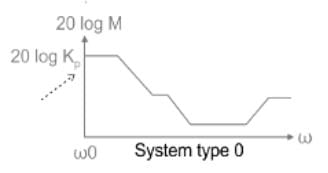
Find the transfer function, from the given plot with a correction of 8dB at ω= 80 rad/sec.
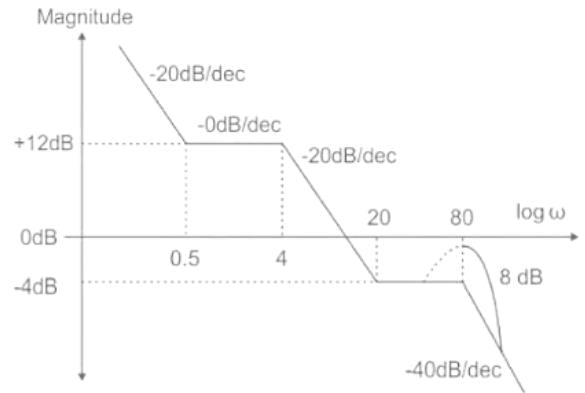

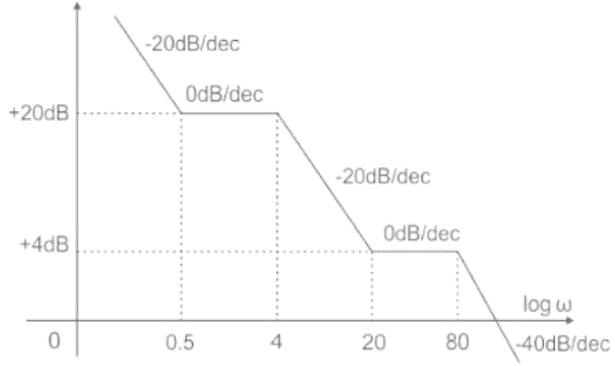
The asymptotic bode plot of a system is shown in figure. Find the expression for its transfer function in frequency domain -

Bode plot consists of two separate plots, one of which consists of -
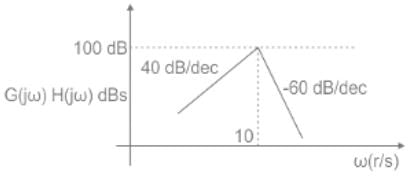
The asymptotic Bode magnitude plot of a minimum phase transfer function G(s) is shown below.
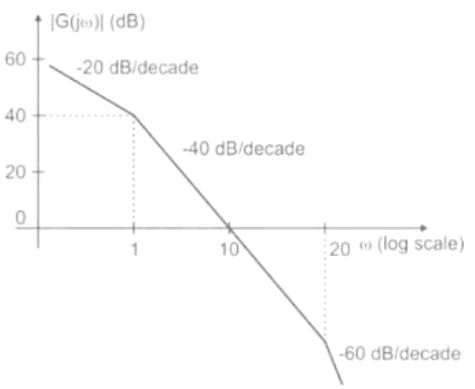
Consider the following two statements.
Statement I: Transfer function G(s) has three poles and one zero.
Statement II: At very high frequency (ω→∞), the phase angle ∠G (jω) = −3π/2.
Which one of the following options is correct?
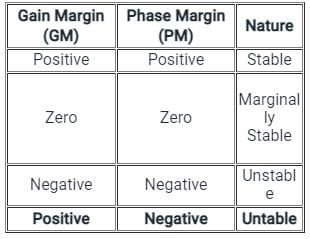
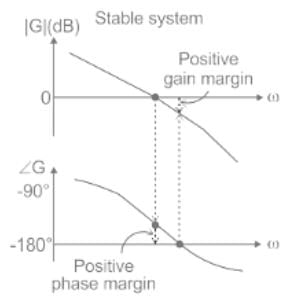
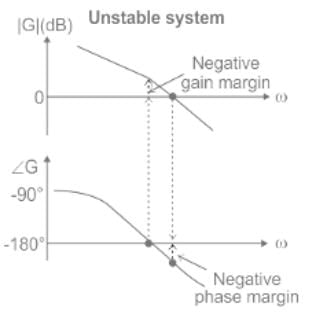
When the gain margin is positive and phase margin is negative, the system is:
The transfer function of a system is 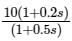
The corner frequencies will be
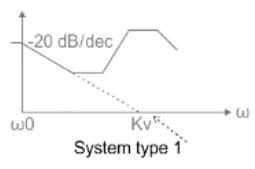
If the given system is connected to a unity negative feedback system, the steady-state error of a closed-loop system to a ramp input is;
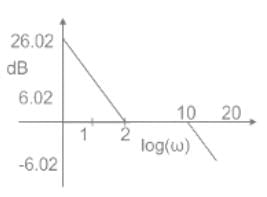
The unit circle of the Nyquist plot transforms into unity or 0 dB line of the amplitude plot of the Bode diagram for
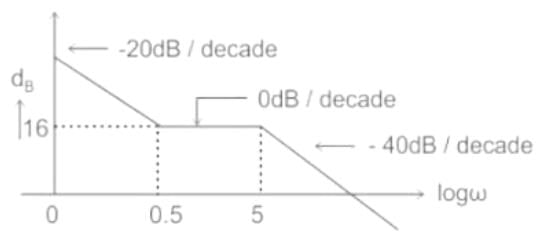
Which one of the following transfer functions represents the Bode plot as shown in the figure (where K is constant)?