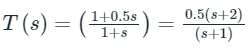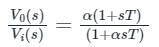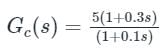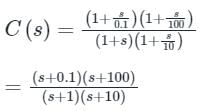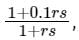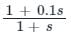Test: Compensators - 2 - Electrical Engineering (EE) MCQ
14 Questions MCQ Test - Test: Compensators - 2
Direction: The following item consists of two statements, one labelled as ‘Statement (I)’ and the other as ‘Statement (II)’. Examine these two statements carefully and select the answers to these items using the code given below:
Statement I: For type-II or higher systems, lead compensator may be used.
Statement II: Lead compensator increases the margin of stability.
Statement II: Lead compensator increases the margin of stability.
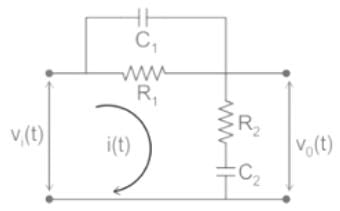
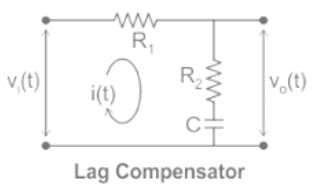
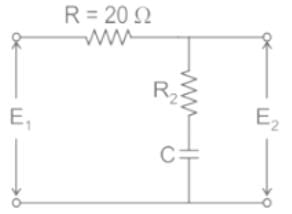
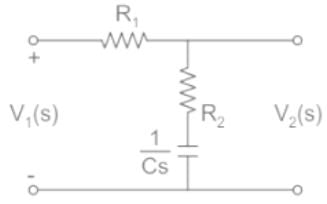
For the following network to work as lag compensator, the value of R2 would be

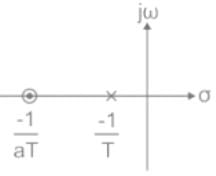
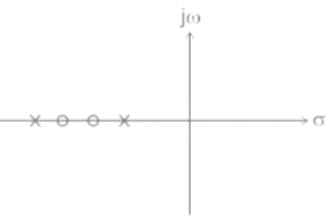
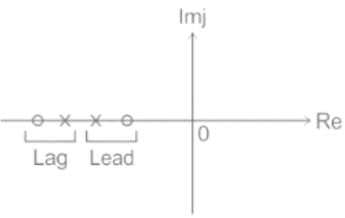
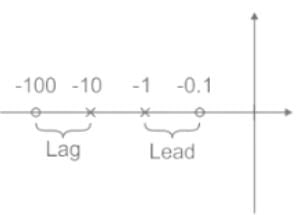
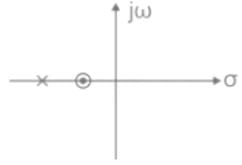
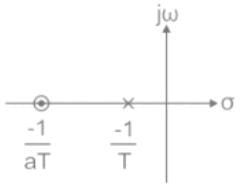
Which of the following can be the pole-zero configuration of a phase-lag controller (lag compensator)?
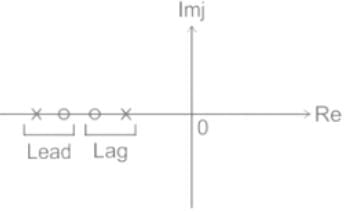
The Transfer Function of lead and lag compensators have _____ and ______ phase angles respectively which the system ______ and ______ respectively.
Which of the following is NOT the disadvantage of lag compensator in a control system?
If the transfer function of a compensator is represented as:
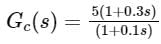
How much maximum phase shift can it add to the system?
The transfer function C(s) of a compensator is given below.
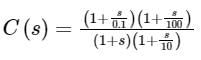
The frequency range in which the phase (lead) introduced by the compensator reaches the maximum is
In the phase lead compensation network, the phase of ______ leads the phase of ______.
If r = 1 in the G(s) = 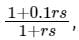 then the compensator can give the minimum phase at a frequency of
then the compensator can give the minimum phase at a frequency of


 then a < 1
then a < 1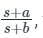 then a > b
then a > b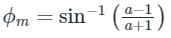

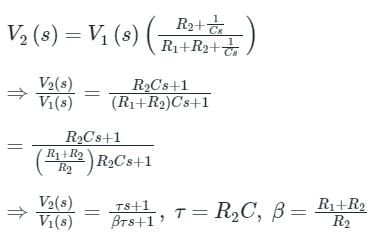 The above system to be lag compensator, β > 1
The above system to be lag compensator, β > 1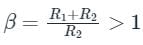
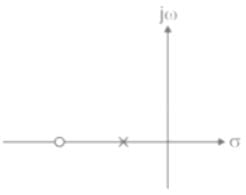
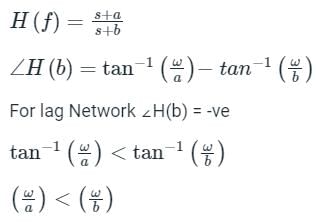
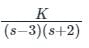
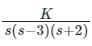
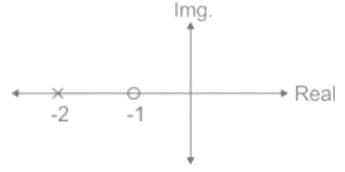
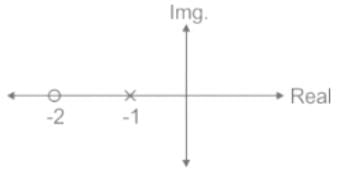
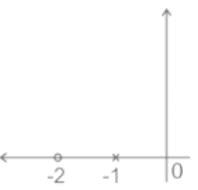
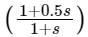 represents a
represents a then a < 1
then a < 1 then a > b
then a > b