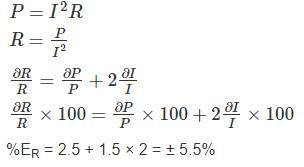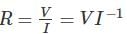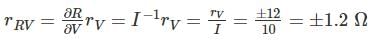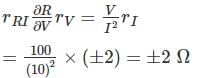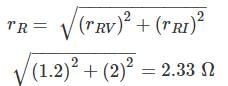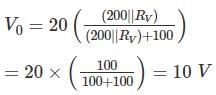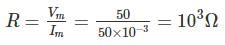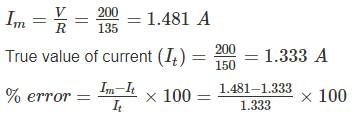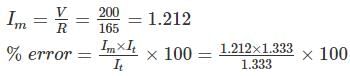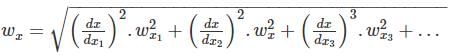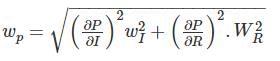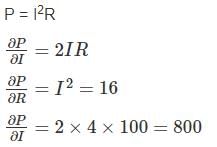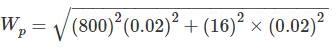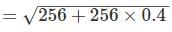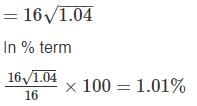Test: Electrical & Electronic Measurements- 1
10 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Electrical & Electronic Measurements- 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The resistance of the circuit is found by measuring current flowing and power fed into the circuit. If limiting errors in the measurement of power and current are ± 2.5% and ± 1.5%. Respectively, the limiting error in the measurement of resistance will be _______ (in percentage)
The battery voltage of an analog multimeter drops by 20% of its original value. The multimeter is used to measure dc voltage of a circuit. The true voltage compared to the measured value is
The internal battery of an analog multimeter is used to find resistance. The battery voltage doesn’t influence the measurement of voltage. Hence, the true value and measured value both are same.
A 50 V range voltmeter has a sensitivity of 40 KΩ/V. The total resistance of the voltmeter is – (in MΩ)
Given that,
Voltage range = 50 V
Sensitivity = 40 KΩ/V
Total resistance = Sensitivity × Voltage range
= 40 KΩ/V × 50 V
= 2000 KΩ
= 2 MΩ
A voltmeter has 100 scale divisions and can measure up to 200 V. Each division can be read up to 1/5 division. The resolution of the voltmeter is – (in V)
100 divisions = 200 V
1 divisions = 2 V
1/5 division = 0.4 V
Resolution = 0.4 V
A resistance is determined by voltmeter ammeter method. The voltmeter reads 100 V with a probable error of ±12 V and ammeter reads 10 A with a probable error of ±2 A. Determine the probable error in the computed value of resistance
We have resistance 
Weighted probable error in the resistance due to voltage is,
Weighted probable error in the resistance due to current is,
Probable error in computed resistance is,
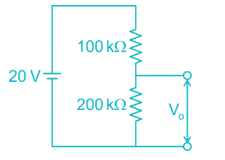
A voltage reading is to be taken across the load Resistor RL in the circuit shown below. A voltmeter with a sensitivity 10 kΩ/V and a guaranteed accuracy of ± 5 % at full scale is to be used on its 20 V range. The maximum voltmeter reding that could be expected is __ (in V)
Sensitivity of voltmeter = 10 kΩ/V
Full scale reading (VFSD) = 20 V
Internal resistance of voltmeter (Rv) = 10 kΩ/V × 20 V
= 200 kΩ
By voltage division,
Guaranteed accuracy of meter = ± 5% at FSD.
V0 = 10 ± (5% of 20) = 10 ± 1 = 9 to 11
Maximum voltmeter reading = 11 V.
The resistance is measured by the voltmeter ammeter method the voltmeter reding is 50 V on 100 V scale and ammeter reading is 50 mA on 100 mA scale. If both the meters are guaranteed for accuracy with 2% of full scale, what is the limit within which resistance (in Ω ) can be measure?
V = 50 ± (2% of 100 V)
Im = 50 × 10-3 ± (2% of 100 mA)
Rm = 103 ± 4% = 1000 ± 40
= 960 Ω to 1040 Ω
Limit = 80 Ω
A 150 ± 10% Ω resistor is connected to the terminals of a power supply operating at 200 ± 0V. If the resistor varies over the range ± 10% of its expected value, what is the range of error in this current.
Given voltage range, V = 200 ± 0 V
Given resistor range, R = 150 ± 10% Ω
= [150 – 10%, 150 + 10%]
= [150 – 15, 150 + 15]
= [135, 165] Ω
When R = 135 Ω
= 11.13%
When R = 165 Ω
= -9.07%
Range of error in the current = -9.07% to 11.13%
Which one of the following statement is not correct?
It is possible to have precise measurements which are not accurate. we can get precise results which may not accurate.
So option (a) is not correct
The current I flowing through a resistance of value 100 Ω ± 0.2% is I = 4A ± 0.5% the uncertainty in measurement of power is
When many variables are in valued is done on the same basis as is done for error analysis when the result are expressed as standard deviation or probable errors.
Let x = F(x1, x2, x3 …..)
Wx1, Wx2, …. Wxn be the uncertainties of x1, x2, … xn then uncertainty of x is given by
Calculation:
R = 100 ± 0.2% = 100 ± 0.2
I = 4 ± 0.5% = 4 ± 0.2
P = 100 × 42 = 1600 W
|
22 docs|274 tests
|
Up next
|
22 docs|274 tests
|
Up next
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
