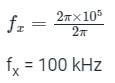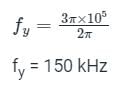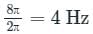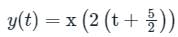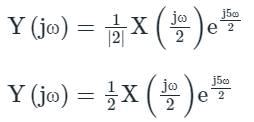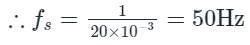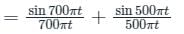Test: Sampling Theorem and Nyquist Rate - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Sampling Theorem and Nyquist Rate
The highest frequency component of a speech signal needed for telephonic communications is about 3.1 kHz. What is the suitable value for the sampling rate?
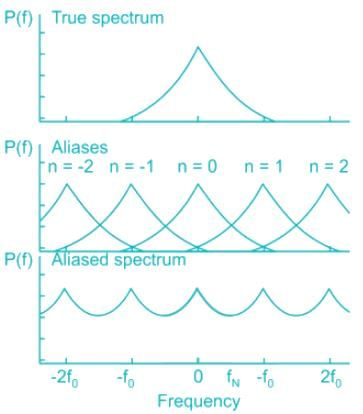
A single tone 4 kHz message signal is sampled with 9 kHz, 7 kHz and 5 kHz. Aliasing effect will be seen in the reconstructed signal, when the signal is sampled with
The figure given below shows the Fourier spectra of signal x(t) and y(t).
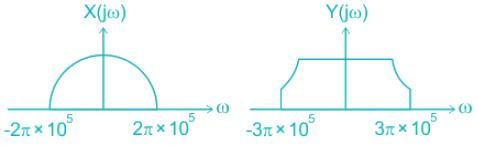
The Nyquist sampling rate for x(t) y(t) is_________.

The Nyquist sampling rate for x(t) y(t) is_________.
Consider the signal x(t) = cos(6πt) + sin(8πt), where t is in seconds. The Nyquist sampling rate (in samples/second) for the signal y(t) = x(2t + 5) is
A continuous-time signal has frequency content at f = 10 MHz, 50 MHz, and 70 MHz. The signal is sampled at a sampling frequency of 56 MHz and is then passed through a low-pass filter with a cutoff frequency of 15 MHz. The frequency content of the output of the filter will be:
A sinusoid x(t) of unknown frequency is sampled by an impulse train of period 20 ms. The resulting sample train is next applied to an ideal lowpass filter with cutoff at 25 Hz. The filter output is seen to be a sinusoid of frequency 20 Hz. This means that x(t) is
An input signal x(t) = 2 + 5sin(100πt) is sampled with a sampling frequency of 400 Hz and applied to the system whose transfer function is represented by
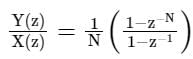
where, N represents the number of samples per cycle. The output y[n] of the system under steady state is
If a 100 Hz sinusoidal signal is sampled at the rates of 140 Hz, 90 Hz, and 30 Hz, then the aliased frequencies correspond to each sampling rate will be respectively:
The Nyquist sampling interval, for the signal sinc(700t) + sinc(500t) is:
A band-limited signal with a maximum frequency of 5 kHz is to be sampled. According to the sampling theorem, the sampling frequency which is not valid is