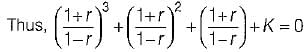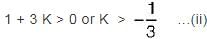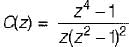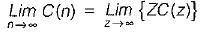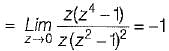Test: Stability Analysis of Linear Control Systems- 2 - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test - Test: Stability Analysis of Linear Control Systems- 2
Which of the following is the correct statement?
A minimum phase network is one whose transfer function has
A minimum phase network is one whose transfer function has
For a discrete-time system to be unstable, all the poles of the z-transfer function should lie
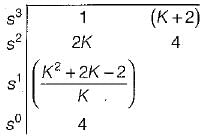
Consider the following characteristic equation of a system:
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?
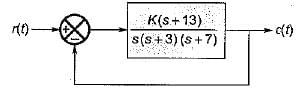
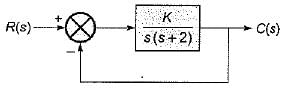
For which of the following values of K, the feedback system shown in the below figure is stable?
What is the range of K for which the open loop transfer function
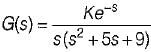
represents an unstable closed loop system?
What is the range of values of K (K > 0) such that the characteristic equation
s3 + 3 (K + 1)s2 + (7K + 5)s + (4K + 7) = 0
has roots more negative than s = -1?
A closed loop control system is shown below:
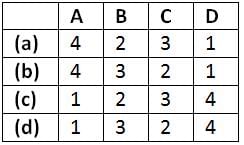
Match List - I (Different values of K) with List - II (Roots of Characteristic Equation) and select the correct answer using the codes given below the lists:

Codes:
Consider the following statements regarding the characteristic equation of a system given by:
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?
The transfer function of a system is (1 + 2s)/(1 - s)
The system is then which one of the following?
Assertion (A): For a system to be stable, the roots of the characteristic equation should not lie in the right half of the s-plane or on the imaginary axis.
Reason (R): A system is said to be stable if the zeros of the closed loop transfer function are all in the left half of s-plane.
Assertion (A): Location of the poles of a transfer function in the s-plane affects greatly the transient response of the system and hence stability.
Reason (R): The poles that are close to the imaginary axis in the left-half s-plane give rise to transient responses that will decay relatively slowly, whereas the poles that are far away from the axis (relative to the dominant poles) correspond to fast-decaying time responses.
Assertion (A): Routh-Hurwitz criterion doesn’t provides the information about the number of roots that lie on the jω-axis while it tests whether any of the roots of the characteristic equation lie in the right-half s-plane or not.
Reason (R): The Routh-Hurwitz criterion represents a method of determining the location of zeros of a polynomial with constant real coefficients with respect to the left half and right half of the s-plane, without actually solving for the zeros.
Consider the following statements related to Routh-Hurwitz criterion of determining the stability of a system:
1. It is applicable if the characteristic equation has real coefficients, complex terms or exponential functions of s.
2. The criterion can be applied to any stability boundaries in complex plane, such as the unit circle in the z-plane.
3. The number of changes of signs in the elements of the first column equals the number of roots with negative real parts.
Which of these statements is/are not correct?
The characteristic equation of a linear discrete-data control system is given as:
F(z) = z3 + z2 + z + K = 0,
Where K is a real constant.
What is the range of values of K so that the system is stable?
The characteristic equation of a linear time-invariant discrete-data system is given by:
F(z) = anzn + an - 1 zn - 1 + .......... + a1 z + a0 = 0
where all the coefficients are real.
According to “Jury’s stability criterion”, there are certain necessary conditions which must be satisfied for the above discrete-data system to have no roots on or outside the unit circle.
Which of the following necessary condition does not holds true for the discrete-data system to have all roots inside the unit circle according to “Jury's stability criterion"?
The first two rows of Routh’s tabulation of a third-order system are
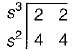
Select the correct answer from the following choices.
The characteristic equation of a second order discrete-data system is given by:
F(z) = z2+ z+ 0.25 = 0
The above system is
The z-transform of a signal is given by:
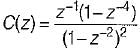
Its final value is
The dynamic response of a system is given by the following differential equation:
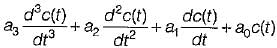
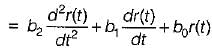
where c(t) and r(t) are respectively the output and the input and a3 , a2 , a1 a0, b2, b1 and b0 are constants. It is a
The transfer function of a system is:
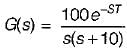
The system


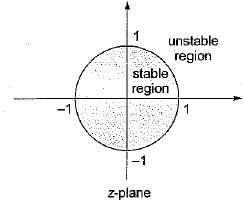

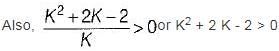
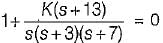

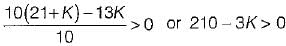
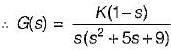



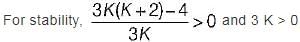
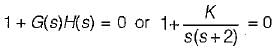
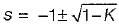
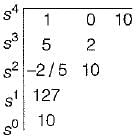
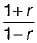 in the above characteristic equation.
in the above characteristic equation.