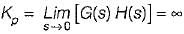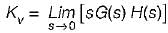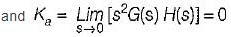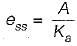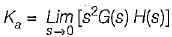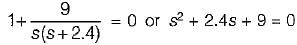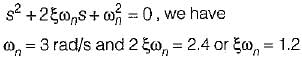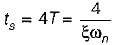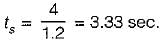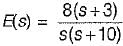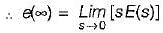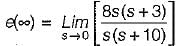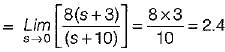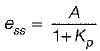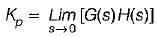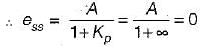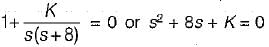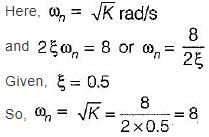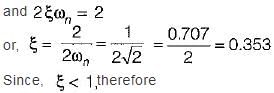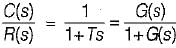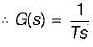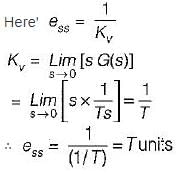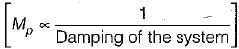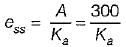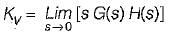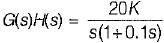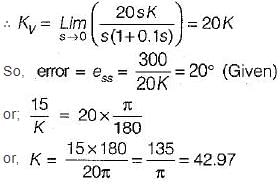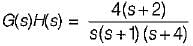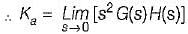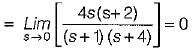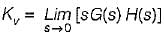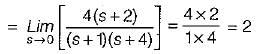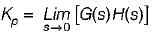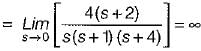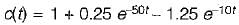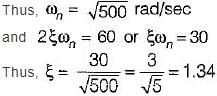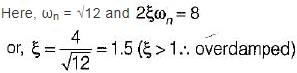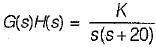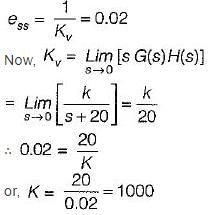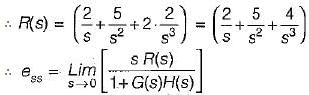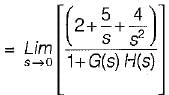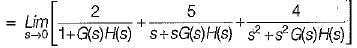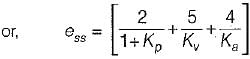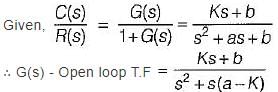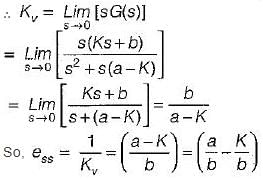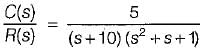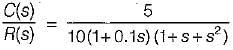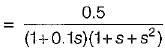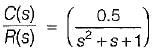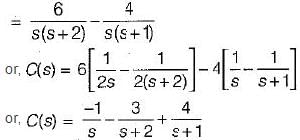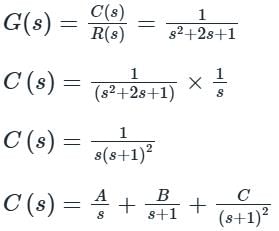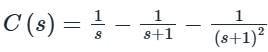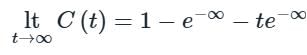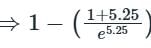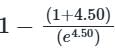Test: Time Domain Analysis of Control Systems- 2 - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test - Test: Time Domain Analysis of Control Systems- 2
The steady-state error coefficients for a system are Kp = ∞ , Kv = finite constant and Ka = 0. The type of the system is
The steady-state error of a feedback control system with an acceleration input becomes finite in a
Consider the unity feedback system shown below:
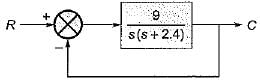
The settling time of the resulting second order system for 2% tolerance band will be

The settling time of the resulting second order system for 2% tolerance band will be
For a control system, the Laplace transform of error signal e(t) is given by 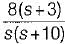 . The steady state value of the error will be
. The steady state value of the error will be
For a type one system, the steady-state error due to step input is equal to
For an unity feedback control system with 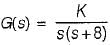 the value of K for damping ratio of 0.5 is
the value of K for damping ratio of 0.5 is
The damping ratio of a system having the characteristic equation s2 + 2s + 8 = 0 is
The closed-loop transfer function of a unity - feedback system is given by 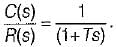 The steady state error to a unit ramp input is:
The steady state error to a unit ramp input is:
The peak overshoot of step-input response of an underdamped second-order system is an indication of
Consider the position control system shown below:
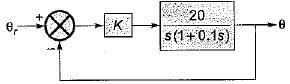
The value of K such that the steady state error is 20° for input θr = 300t rad/sec, is
Assertion (A): With the increase in bandwidth of the system the response of the system becomes fast.
Reason (R): Damping ratio of the system decreases with the increase in bandwidth.
For the stable system described by the block diagram shown below, Match List - I (Static error coefficients) with List - II (Values) and select the correct answer using the codes given below the lists:
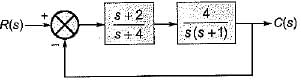
List-I
A. Ka
B. Kv
C. Kp
List-II
1. ∞
2. 0
3. 2
4. -1
Codes:
The unit step response of a system is given by c(t) - 1 + 0.25 e-50t - 1.25 e-10t
The given system is
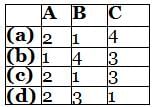
Match List - I (Transfer function of systems) with List - II (Nature of damping) and select the correct answer using the codes given below the lists:

Codes:
The block diagram of an electronic pacemaker is given in figure below.
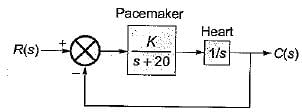
What is the value of K for which the steady-state error to a unit ramp input is 0.02?
Which one of the following equations gives the steady-state error for a unity feedback system excited by r(t) = 2 + 5t + 2t2 ?
An unity feedback control system with closed loon transfer function is given by
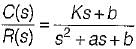
The steady state error due a unit ramp input response is
The second order approximation using dominant pole concept for the transfer function
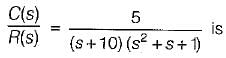
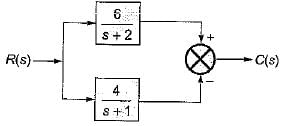
The unit step response of the system represented by the block diagram shown below is
Consider a causal second-order system with the transfer function 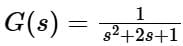 with a unit-step
with a unit-step 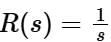 as an input. Let c(s) be the corresponding output. The time taken by the system output c(t) to reach 94% of its steady-state value
as an input. Let c(s) be the corresponding output. The time taken by the system output c(t) to reach 94% of its steady-state value 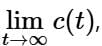 rounded off to two decimal places, is
rounded off to two decimal places, is