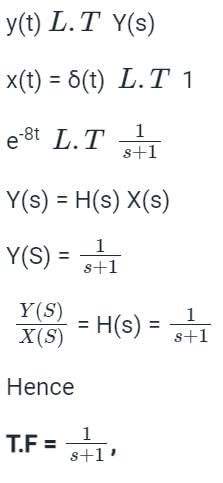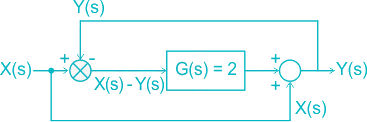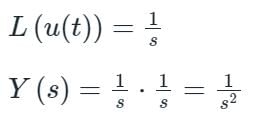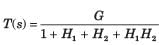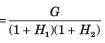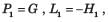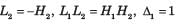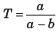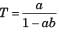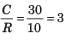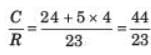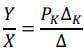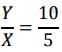Test: Transfer Function - 1 - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test - Test: Transfer Function - 1
The output of the feedback control system must be a function of:
The unit impulse response of a certain system is found to be e-8t. Its transfer function is _______.
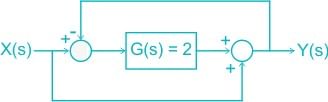
For the system shown in the figure, Y(s)/X(s) = _________. (Answer in integer )
Assuming zero initial condition, the response y(t) of the system given below to a unit step input u(t) is
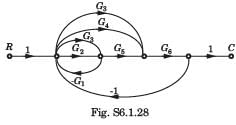
The sum of the gains of the feedback paths in the signal flow graph shown in fig. is
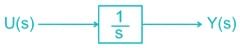
A linear system with H(s) = 1/s is excited by a unit step function input. The output for t > 0 is given by
The overall transfer function C/R of the system shown in fig. will be:
For the signal flow graph shown in fig. an equivalent graph is
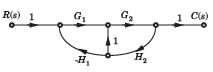
The block diagram of a system is shown in fig. The closed loop transfer function of this system is
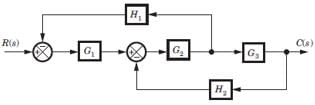
For the system shown in fig. transfer function C(s) R(s) is
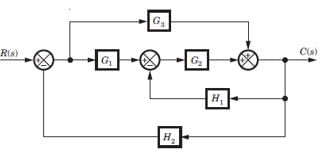
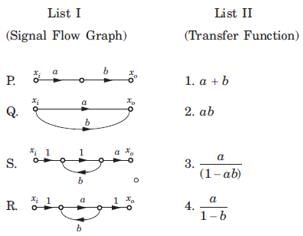
In the signal flow graph shown in fig. the transfer function is
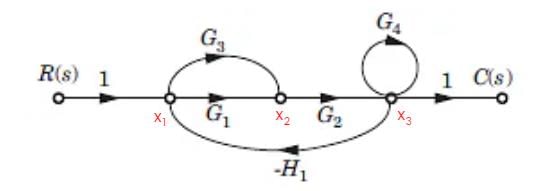
In the signal flow graph shown in fig. the gain C/R is
The gain C(s)/R(s) of the signal flow graph shown in fig.
The negative feedback closed-loop system was subjected to 15V. The system has a forward gain of 2 and a feedback gain of 0.5. Determine the output voltage and the error voltage.
For the block diagram shown in fig. transfer function C(s)/R(s) is
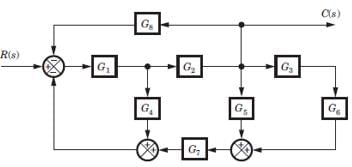
For the block diagram shown in fig. the numerator of transfer function is
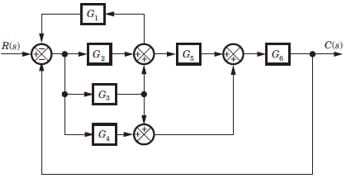
For the block diagram shown in fig. the transfer function C(s)/R(s) is