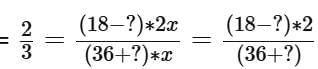Test: Data Insights - 8 - GMAT MCQ
20 Questions MCQ Test GMAT Mock Test Series 2025 - Test: Data Insights - 8
Which one of the following statements most accurately describes a relationship between the table and the introduction?
For each of the following statements about Nation X, choose Yes if it describes a situation that the given information suggests may have resulted from the experimental incentive scheme. Otherwise, choose No.
For each of the following statements about Nation X, select Consistent if the statement is consistent with the information provided. Otherwise, select Inconsistent.
Each of three botanists made a hypothesis regarding specimens of a particular plant species:
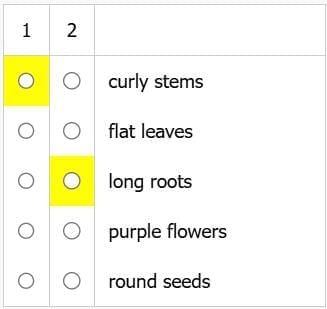
- Botanist 1: Any individual specimen possessing the gene for curly stems has either the gene for long roots or the gene for purple flowers, or both.
- Botanist 2: Any individual specimen possessing the gene for long roots has either the gene for flat leaves or the gene for round seeds, or both.
- Botanist 3: No individual specimen that possesses either the gene for curly stems or the gene for flat leaves or both has the gene for purple flowers.
The discovery of an individual specimen of the plant species in question having the gene for __1__ but NOT the gene for __2__ would show that at least one of the three hypotheses described is incorrect.
Choose for 1 and for 2 the characteristics that would most accurately complete the statement, based on the information given. Make only two selections, one in each column.
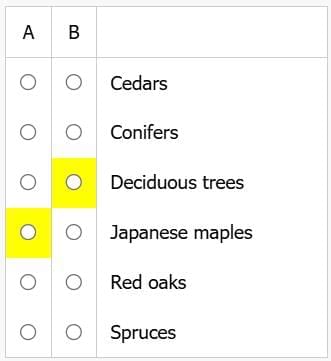
An inventory of a neighborhood's trees found that 32 percent were conifers and most of the rest were deciduous. Among the conifers were 258 spruces and 112 pines, along with some cedars and other species. Most of the deciduous trees were oaks, but one in eight was a maple. Of the oaks, 65 percent were red oaks and 25 percent were white oaks. Of the maples, 20 percent were Japanese maples.
Choose for A and for B two types of trees such that the ratio of the number of trees of the type choose for A to the number of trees of the type choose for B can be determined and is less than 1. Make only two selections, one in each column.
Throughout a certain decade in a European city, the mean monthly rents for studio apartments varied yearly, from a low of €804 to a high of €1,173. Those for one-bedroom apartments also varied yearly, from a low of €1,060 to a high of €1,497. But some individual studio apartments rented for as little as €420 in some years, and some one-bedroom apartments rented for up to €2,262. To visually assess how the ratio of mean monthly rents for studio apartments to those for one-bedroom apartments varied yearly over the decade, Maria requires a graph with the following characteristics. The graph will have two axes of equal length, with mean rents for one-bedroom apartments shown on the horizontal axis and mean rents for studio apartments shown on the vertical axis, and with the same scale on both axes. For each year, mean rents will be plotted as a point.
From the following options, choose for Horizontal axis a range for the points on the horizontal axis and choose for Vertical axis a range for the points on the vertical axis that together would satisfy Maria's requirements for the graph. Make only two choose, one in each column.
For every dollar of sales charged to a certain bank credit card, a department store must pay $0.003 to the bank that issued the credit card. What percentage of the department store's sales transactions last month were credit card transactions?
(1) The store made 2,000 sales last month.
(2) The store took in a total of $250,000 last month and paid $300 to the bank that issued the credit card.
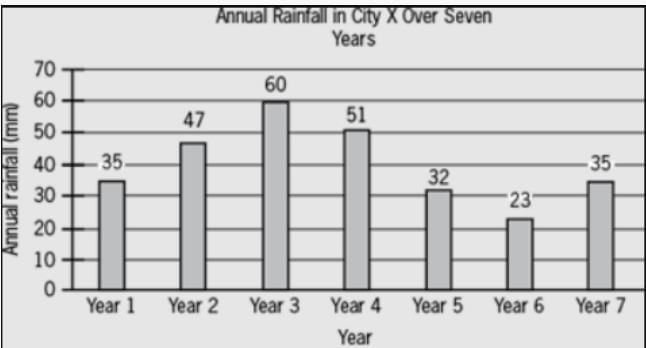
The annual rainfall in a city over the past 50 years is its historical average rainfall (HAR). The graph above shows the annual rainfall in City X over a seven-year period. All figures are rounded to the nearest integer.
Is it true that the rounded HAR for City X is 47 mm or greater?
(1) In the seven-year period in City X, the annual rainfall was greater than the HAR in exactly two of the consecutive years.
(2) In the seven-year period in City X, the annual rainfall was less than the HAR in exactly four of the years.
On a farm with a total of 72 animals, some are goats, and the rest are cows. If there is at least one goat and at least one cow, what is the positive difference between the number of vaccinated goats and vaccinated cows?
(1) One-fourth of the goats and one-ninth of the cows are vaccinated.
(2) The ratio of vaccinated goats to vaccinated cows is 9 to 4.
Rosalie tosses a coin a number of times and counts the total number of times the coin lands tail-side up. How many times does she toss the coin?
(1) The chance that the coin lands tail-side up exactly once is between 0.1 and 0.2.
(2) The chance that the coin lands head side up exactly once is the same as the chance that the coin lands tail-side up exactly once.
Mrs. Claus is selecting three reindeer from the herd for a special sleigh ride. Among the herd are Rudolph, Blitzen, and Comet. What is the probability that she chooses Rudolph, but not Blitzen and not Comet?
(1) The probability that she chooses Rudolph and Blitzen, but not Comet, is 1/14.
(2) The probability that she chooses none of Rudolph, Blitzen, and Comet is 5/21.
There are three different ways to score in basketball. A successful shot from beyond an arc drawn on the court is worth 3 points. Shots made from inside the arc are worth 2 points. If a player is fouled by another player, the fouled player may shoot "free throws," which are worth 1 point each. A certain team scored 45 points in a game. The team made twice as many 2-point shots as 3-point shots. How many free throws did the team make?
(1) The team attempted 12 free throws.
(2) Five-sixths of the team's free-throw attempts were successful.
When David drove from his home to his parents' home, was his average speed between 35 miles per hour and 50 miles per hour?
(1) To the nearest 100 miles, the distance that David drove from his home to his parents' home was 300 miles.
(2) To the nearest hour, it took David 8 hours to drive from his home to his parents' home.
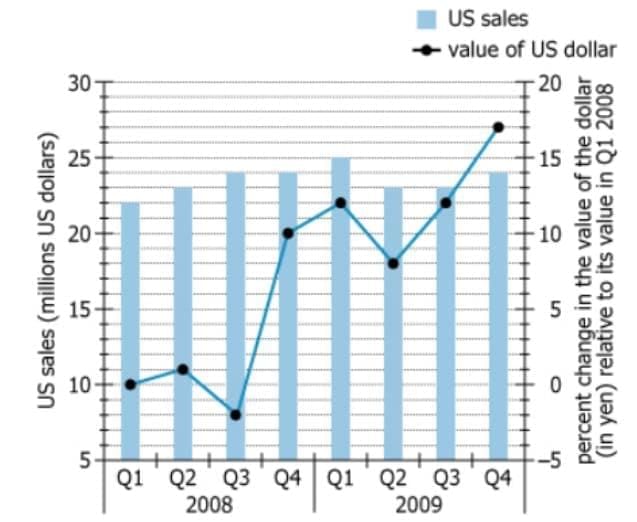
For each of the 8 quarters of 2008-2009, the graph shows a Japanese electronics firm ́s total US sales (rounded to the nearest 1 million US dollars), and the change in the average value of US dollar in Japanese yen, where the change is expressed as a percentage of the dollar ́s value in the first quarter of 2008 (Q1 2008), to the nearest 1 percent. For any given quarter, this data may be used to convert total US sales to their Q1 2008 yen equivalent: a value directly proportional to that quarter ́s total US sales in Q1 2008 yen.
On the basis of the information provided, choose the option that created the most accurate statement.
Q1 2008 yen-equivalent sales were highest in ___(A)___ of 2009.
Q1 2008 yen-equivalent sales for Q4 2009 were __(B)____ Q1 2008 yen-equivalent sales for Q4 2008.
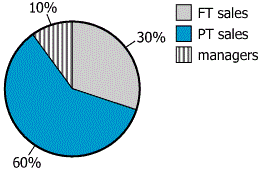
A retail store has 60 employees—full-time salespeople (FT sales), part-time salespeople (PT sales), and managers—in the proportions shown by the graph. Each full-time salesperson and each manager works the same number of hours per week; each part-time salesperson works exactly half that many hours per week.
The store wants the ratio of the total number of hours worked per week by full-time salespeople to the total number of hours worked by part-time salespeople to be 2:3 and wants to achieve this ratio without changing the number of managers or the number of hours each manager works per week.
Based on the information provided, choose creates the most accurate statement.
To achieve the desired ratio, the store could __(A)___ the number of full-time salespeople and ___(B)___ the number of part-time salespeople.
The designers of a video game hired 100 game testers to play the game to determine whether the level of difficulty was appropriate. Each of the 100 testers made at most 25 attempts to complete each of the game's 15 levels (Levels 1–15). When a tester completed a level, he or she then made no further attempts at that level. For each of the levels, the table shows, among the testers who completed the level, the total number of testers whose number of attempts to complete that level fell in various ranges.
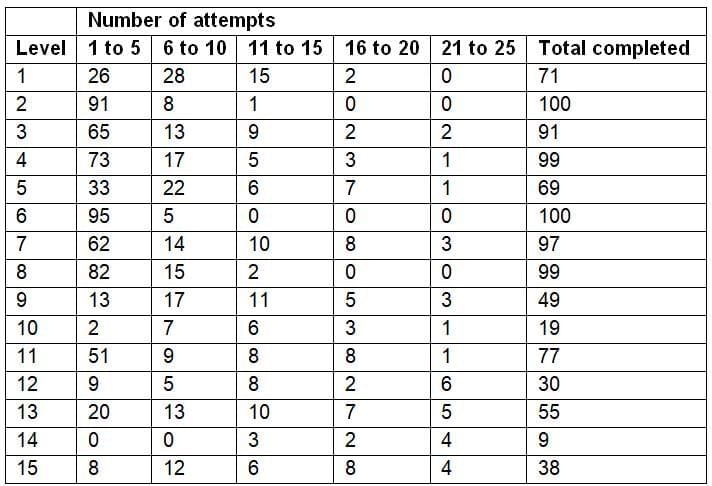
For each of the following statistical measures, select Must be 20 or less for every level if, based on the information provided, the measure must be at most 20 for each of the 15 levels. Otherwise, select Could be greater than 20 for one or more.
Could be greater than 20.
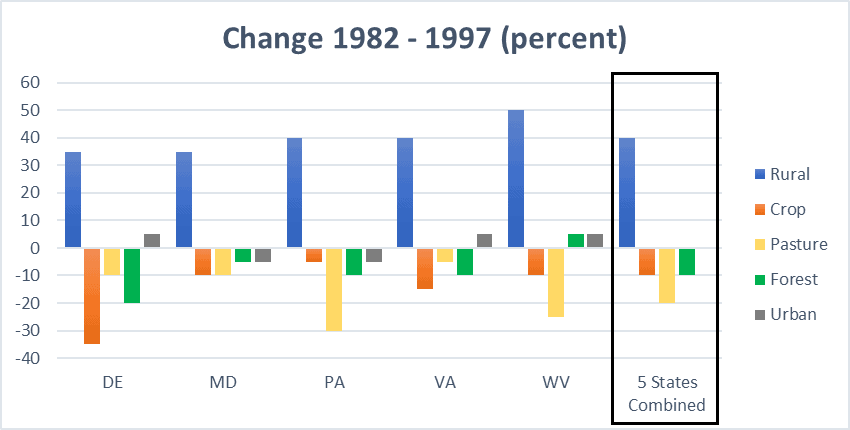
The graph above shows the changes in major land cover types in the given five-state region from 1982 to 1997.
The graph shows the percent change in the area of different land cover types across five states (DE, MD, PA, VA, and WV) as well as for these five states combined, from 1982 to 1997.
Choose the option that creates the most accurate statement based on the information provided.
If in 1997 Pennsylvania's (PA) rural land coverage equaled the average rural land coverage of the five states combined, then in 1982 Pennsylvania's rural land coverage was __(A)__ of the combined rural land coverage for all five states.
If Delaware (DE) and Maryland (MD) had similar acreage of land under crop in 1997, Delaware would have had approximately __(B)___ more acreage of cropland as compared to that in Maryland in 1982.
acres. Therefore, in 1982, Delaware (140 acres) had 40% more cropland acreage than Maryland (100 acres).
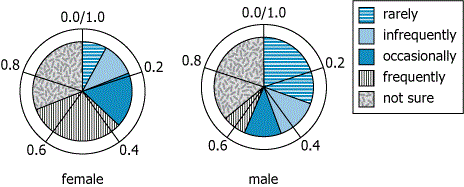
The two charts show how female and male survey respondents answered a question about how often they ate a certain type of food. The survey specified that "infrequently" meant more often than "rarely" but less often than "occasionally."
Choose the options that create the statement that most accurately reflects the information provided.
Slightly less than __(A)__ respondents indicated that they ate the food at most ___(B)___.
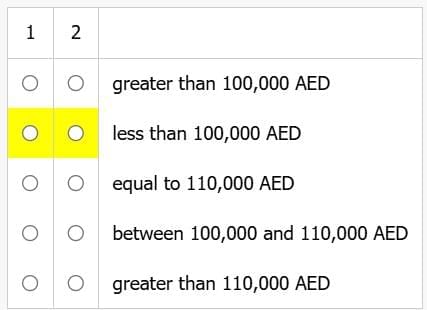
Companies A and B are part of the same industry and are located in the same city. For Company A, the average (arithmetic mean) salary of its employees, in United Arab Emirates dirhams (AED), is 10,000 AED higher than that for Company B. However, more than half of the employees at Company A have salaries below the average for Company B.
Statement: If the average salary at Company B is ___1___, then the median salary at Company A is ___2___.
Select for 1 and for 2 the options that complete the statement so that it most accurately reflects the information provided. Make only two selections, one in each column.
A statistician reached the following conclusions about games between university soccer teams: Overall, a team playing on its home field has a 45% chance of a win, a 25% chance of a loss, and a 30% chance of a draw (a tied outcome). In the games where one or more goals are scored, the team that scores the first goal has a 55% chance of scoring it in the game's first half and a 45% chance of scoring it later in the game. When that team is the home team (i.e., a team playing on its home field), there is a 40% chance that the other team will score no goals at all, and therefore a 60% chance that it will score one or more goals.
Select for X and for Y two different outcomes such that the information provided explicitly includes the statistician's estimates of the probability that if X occurs, so will Y. Make only two selections, one in each column.
|
18 docs|33 tests
|
Important Questions for Data Insights - 8
Data Insights - 8 MCQs with Answers
Online Tests for Data Insights - 8 GMAT Mock Test Series 2025
|
© EduRev
|
Education Revolution
|
|
