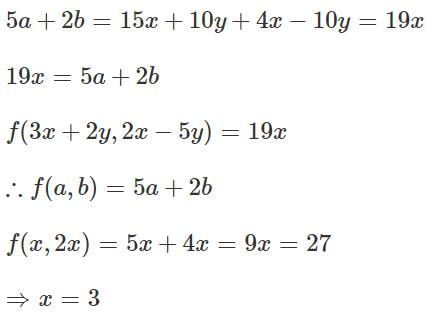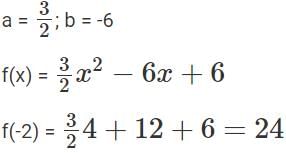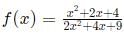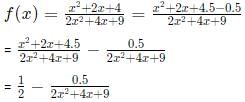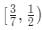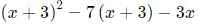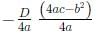CAT Previous Year Questions: Functions (July 9) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - CAT Previous Year Questions: Functions (July 9)
Suppose f(x, y) is a real-valued function such that f(3x + 2y, 2x − 5y) = 19x , for all real numbers x and y . The value of x for which f(x, 2x ) =27, is
[2023]
Let f(x) be a quadratic polynomial in x such that f(x) ≥ 0 for all real numbers x . If f(2)=0 and f(4) = 6 , then f(−2) is equal to
[2022]
For all real values of x, the range of the function 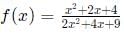 is
is
[2021]
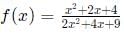 is
isIf x2 − 7x and g(x) = x + 3g(x) = x + 3, then the minimum value of f(g(x)) - 3xf(g(x)) − 3x is:
[2021]
If f ( x + y ) = f ( x) f ( y) and f (5) = 4, then f (10) - f (-10) is equal to
[2020]
For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) - f(m) = 2, then m equals
[2019 TITA]
Consider a function f(x + y) = f(x) f(y) where x , y are positive integers, and f(1) = 2. If f (a + 1) + f (a + 2) + ..... + f(a + n) = 16 (2n - 1) then a is equal to.
[2019 TITA]
Let f be a function such that f (mn) = f (m) f (n) for every positive integers m and n. If f (1), f (2) and f (3) are positive integers, f (1) < f (2), and f (24) = 54, then f (18) equals
[2019 TITA]
If f(x + 2) = f(x) + f(x + 1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals.
[2018 TITA]
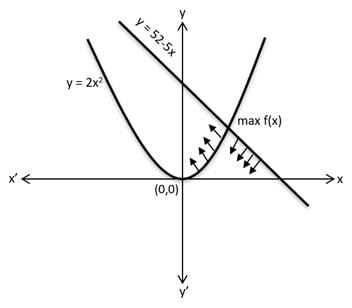
Let f(x) = min{2x2, 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is
[2018 TITA]
|
152 docs|327 tests
|