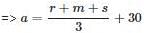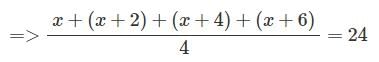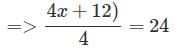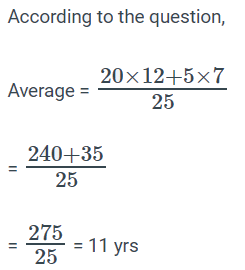Test: Average- 1 - CLAT MCQ
20 Questions MCQ Test - Test: Average- 1
David obtained 76, 65, 82, 67 and 85 marks (out of 100) in English, Mathematics,Physics, Chemistry and Biology What are his average marks ?
The average of 5 consecutive even numbers A, B, C, D and E is 52. What is the product of B and E?
The average weight of 8 persons increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What might be the weight of the new person ?
Average score of Rahul, Manish & Suresh is 63. Rahul's score is 15 less than Ajay and 10 more than Manish. If Ajay scored 30 marks more than the average score of Rahul, Manish & Suresh, what is the sum of Manish's and Suresh's score?
The average of four consecutive odd numbers is 24. Find the largest number.
The average of five positive numbers is 308. The average of first two numbers is 482.5 and the average of last two numbers is 258.5. What is the third number.
Average age of 54 girls in a class was found to be 10 years. It was later on realised that the actual age of one of the girls in the class was 8 years but it was wrongly taken as 18. The actual average age of the girls in the class is
The sum of seven consecutive numbers is 175. What is the sum of the first and the last number
The average marks of nine students in a group is 63. Three of them scored 78, 69 and 48 marks. What are the average marks of remaining six students?
The average age of 20 boys in a class is 12 years. 5 new boys are admitted to the class whose average age is 7 years. The average age of all the boys in the class becomes
The average age of 24 boys and their teacher is 15 years. When the teacher’s age is excluded, the average age decreases by one year. The age of the teacher is
The average of five positive numbers is 213. The average of the first two numbers is 233.5 and the average of last two numbers is 271. What is the third number?
The average weight of 8 men is increased by 1.5 kg when one of them whose weight is 65 kg is replaced by a new man. The weight of the new man is
The average weight of 21 boys was recorded as 64 kg. If the weight of the teacher was added, the average increased by one kg. What was the teacher's weight?
The average height of 16 students in a class is 142 cm. If the height of the teacher is added the average increases by 1 cm. What is the height of the teacher in cm?
The average weight of 15 girls was recorded as 54 kg. If the weight of the teacher was added, the average increased by two kg. What was the teacher's weight.
The average of 7 consecutive numbers is 20. The largest of these numbers is :