Test: Problems on Ages - 5 - CDS MCQ
5 Questions MCQ Test Elementary Mathematics for CDS - Test: Problems on Ages - 5
Father is aged three times more than his son Ronit. After 8 years, he would be two and a half times of Ronit's age. After further 8 years, how many times would he be of Ronit's age?
The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?
A father said to his son, "I was as old as you now at the time of your birth". If the father's age is 38 years now, the son's age five years back was:
A is two years older than B who is twice as old as C. If the total of the ages of A, B and C be 27, the how old is B?
Present ages of Sameer and Anand are in the ratio of 5 : 4 respectively. Three years hence, the ratio of their ages will become 11 : 9 respectively. What is Anand's present age in years?
|
165 videos|95 docs|127 tests
|


 5x = 20
5x = 20 Age of the youngest child = x = 4 years.
Age of the youngest child = x = 4 years.
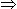 2x = 38.
2x = 38.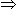 x = 19.
x = 19. Son's age 5 years back (19 - 5) = 14 years.
Son's age 5 years back (19 - 5) = 14 years.
















