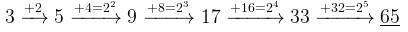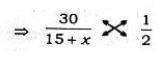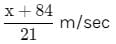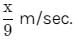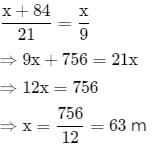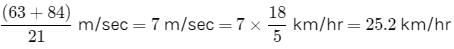Test: Quantitative Techniques- 3
20 Questions MCQ Test Mock Test Series for CLAT | Test: Quantitative Techniques- 3
| 1 Crore+ students have signed up on EduRev. Have you? |
If one-ninth of a certain number exceeds its one-tenth by 4, the number is
x = 360
A coin is tossed thrice. The probability that exactly two heads show up is
As we know that A coin has two faces head and tail.
Total (Exhaustive) number of cases = 23 = 8
Possible outcomes = (HHH, HHT, HTH, THH, HTT, TTH, THT, TTT)
Favourable number of cases = 3
Required probability = 3/8
The angles of a triangle are in the ratio 3 : 4 : 5. The measure of the largest angle of the triangle is
Let the angles be x°
Then,
We know sum of all interior angles of a triangle is 180° so According to problem we must have to find out the value of x° to be correct.
3x + 4x + 5x = 180
⇒ 12x = 180
⇒ x = 180/12
⇒ x = 15
Therefore x° = 15
Here the largest in ratio is 5 so we can write that 5x is the largest angle.
5x = 5×15 = 75°
The sum of three numbers is 98. If the ratio of the first to the second is 2 : 3 and that of the second to the third is 5 : 8, then the second number is
So second no. (B) = 
If the circumference of a circle is reduced by 50%, its area will be reduced by
Reduction in area = πr2−πr2/4 =3πr2/4
% reduction = 3πr2/(4 x πr2) x 100
= 75%
12 persons can do a piece of work in 4 days. How many persons are required to complete 8 times the work in half the time?
The work requires 12 persons x 4 days = 48 person-days.
A work that is 8 times that size will need 48x*8 = 384 person-days.
Now if the work is to be done in 4/2 days or 2 days, we need
384/2 = 192 persons.
Two pipes can fill a tank in 15 hours and 20 hours respectively, while the third can empty it in 30 hours. If all the pipes are opened simultaneously, the empty tank will be filled in
Let the capacity of the tank be 60 units (LCM of 15, 20 & 30).
Pipe A fills = 60/15=4 units / hour
Pipe B fills = 60/20=3 units / hour
Pipe A fills = 60/20=2 units / hour
(A + B + C)'s together per hour work = (4+3−2)=5 units/hour
Time taken by all three to fill an empty tank = 60/5=12 hours.
The next number of the sequence 3, 5, 9, 17, 33, …….is
The cost price of 8 articles is equal to the selling price of 9 articles. The profit or loss per cent in the transaction is
Let the C.P. of each article be 1 Rs.
∴ CP of 9 article = 9 Rs.
∴ SP of 9 article = 8 Rs.
∴ Loss = 1 Rs.
If 78*3945 is divisible by 11. where * is a digit, then * is equal to
We'll apply the divisiblity rule for 11
Odd place: 7+∗+9+5=21+∗
Even place: 8+3+4=15
(21 + *) - (15) = either 11 or 0
(21 + *) - 15 = 11
21 + * = 26
* = 5
In a 45 litres mixture of milk and water, the ratio of the milk to water is 2 : 1. When some quantity of water is added to the mixture, this ratio becomes 1 : 2. The quantity of water added is
Milk : water = 2 : 1
let ratio be 2a and a
so, 2a + a = 45
a = 15
∴ Milk=2×15=30 litres
Water=1×15=15 litres
60 = 15 + x
x = 45 litres
A and B together can do a piece of work in 10 days. A alone can do it in 30 days. The time in which B alone can do it is
(A+B)’s 1 day’s work = 1/10
A’s 1 day’s work = 1/30
∴ B’s 1 day’s work = 1/10 - 1/30
=2/30 = 1/15
Hence B can alone complete the work in 15 days.
If the price of tea is increased by 20%, by how much per cent the consumption of tea be reduced so that there is no increase in the expenditure on it?
Let the original price of the tea be Rs 100.
The price of the tea is increased by 20%.
Increased price of the tea = 100 + (20% of 100) = 100 + 20 = Rs 120.
Increase in price = 120 - 100 = Rs 20
Tea of cost Rs 20 is to decreased out of the increased cost of Rs 120.
Percentage decrease = (20/120) x 100 = 100/6 = 
The smallest 4-digit number, which is a perfect square, is
312=961
322=1024
332=1089
342=1156
Least number of four digits = 1000.
(32)2 is more than 1000 by 24.
So, the least number to be added to 1000 is 24.
1000 + 24 = 1024
Therefore, the smallest four digit number which is a perfect square is 1024.
The difference between a single discount of 30% on Rs. 550 and two successive discounts of 20% and 10% on the same amount is
Ist Discount = 30%
Net two successive Discount =
20+10−(20×10)/100
= 2%
So difference = 2% of 550 = Rs 11
A dealer makes a profit of 20% even after giving a 10% discount on the advertised price of a scooter. If he makes a profit of Rs. 7500 on the sale of the scooter, the advertised price was
According to question
MP = 50,000
A person standing on a railway platform noticed that a train took 21 seconds to completely pass through the platform which was 84 m long and it took 9 seconds in passing him. The speed of the train was
Let the length of the train be x metres
Then Speed of the train in passing through the platform 
and speed of the train in passing the man = 
Since both the speeds are the same,
∴ speed of the train =
then the value of x is7x = 1/343
7x = 1/(73)
7x = 7(- 3)
x = - 3
The average of runs scored by a player in 10 innings is 50. How many runs should he score in the 11th innings so that his average is increased by 2 runs?
Given, The average of runs scored by a player in 10 innings = 50
Let the number of runs scored in 11th innings be n.
According to question ,
∴ 10 × 50 + n = 11 × 52
⇒ 500 + n = 572
⇒ n = 572 – 500 = 72 runs
|
2 videos|9 docs|77 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
2 videos|9 docs|77 tests
|
Download free EduRev App
Related content with Test: Quantitative Techniques- 3
|
|
|
|
Related tests with Test: Quantitative Techniques- 3
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
