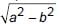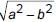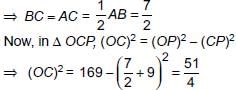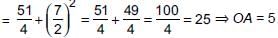Math Olympiad Test: Circles- 4 - Class 10 MCQ
10 Questions MCQ Test Olympiad Preparation for Class 10 - Math Olympiad Test: Circles- 4
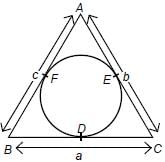
Let s denote the semiperimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, find BD.
Two concentric circles of radii a and b, where a > b, are given. The length of a chord of the larger circle which touches the other circle is
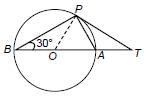
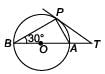
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, then BA : AT is
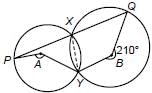
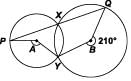
In the given figure, A and B are the centres of two circles that intersect at X and Y. PXQ is a straight line. If reflex angle QBY = 210°, find obtuse angle PAY.
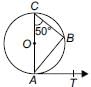
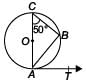
If O is the centre of a circle, AOC is its diameter and B is a point on the circle such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT =
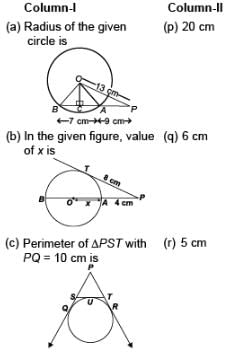
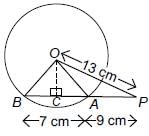
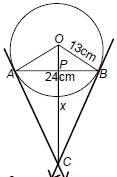
AB is a chord of length 24 cm of a circle of radius 13 cm. The tangents at A and B intersect at a point C. Find the length AC.
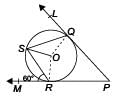
In the given figure, O is the centre of a circle; PQL and PRM are the tangents at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, find ∠QSR and ∠RPQ.
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
|
13 videos|44 docs|187 tests
|