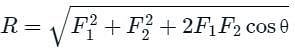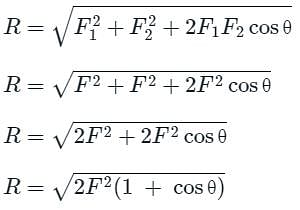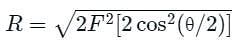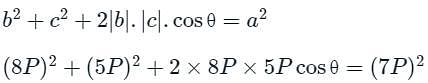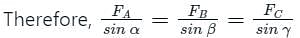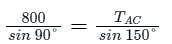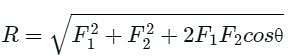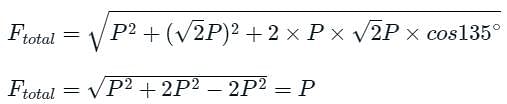Test: Equilibrium of Forces - JEE MCQ
10 Questions MCQ Test Physics for JEE Main & Advanced - Test: Equilibrium of Forces
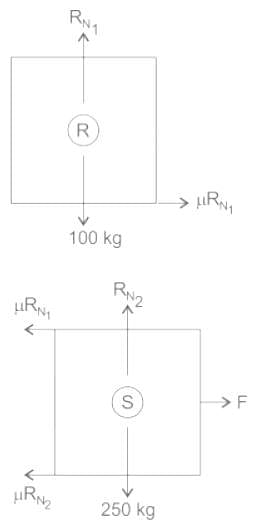
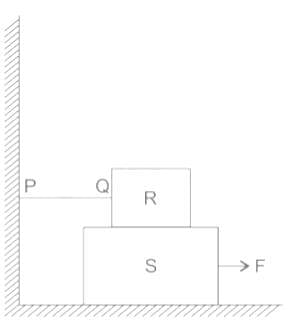
A block R of mass 100 kg is placed on a block S of mass 150 kg as shown in the figure. Block R is tied to the wall by a massless and inextensible string PQ. If the coefficient of static friction for all surfaces is 0.4, the minimum force F (in kN) needed to move the block S is

Two forces of equal magnitude 'F' acts on a particle, and the angle between these forces is θ. Then the resultant of these forces is given by
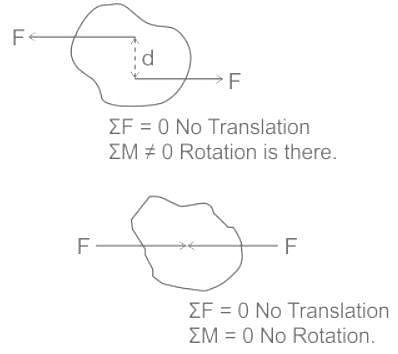
If the sum of all the forces acting on a body is zero, it may be concluded that the body.
A 1 m long uniform beam of 2 kg mass is being lifted vertically up by a force F at the 100 cm mark. What is the minimum force required to do so?

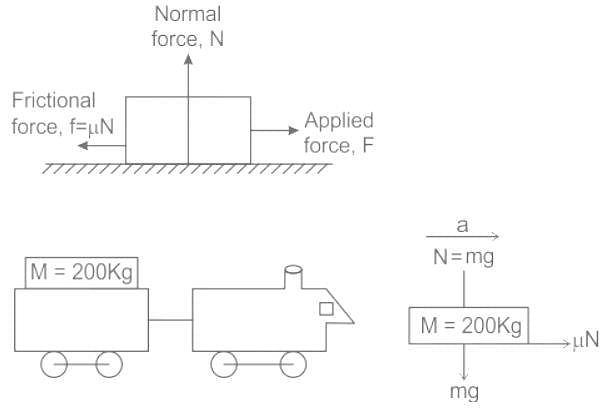
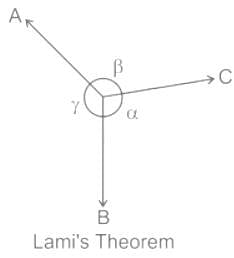
Condition of static equilibrium of a planar force system is written as
Coplanar forces equal to 7P, 8P and 5P acting on a particle are in equilibrium, then the angle between 8P and 5P is:
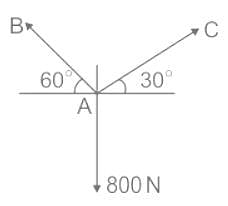
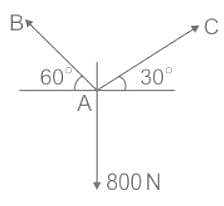
If point A is in equilibrium under the action of the applied forces, the values of tension. TAC = ?
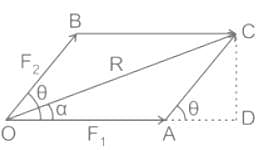
Two forces P and P√2 act on a particle in directions inclined at an angle of 135° to each other. Find the magnitude of the resultant.
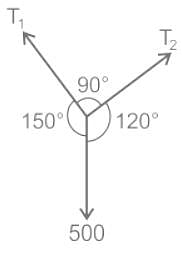
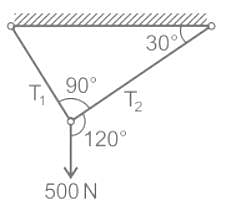
A weight of 500 N is supported by two metallic ropes as shown in the figure. The values of tensions T1 and T2 are respectively:
|
289 videos|635 docs|184 tests
|