Math - 2019 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test IIT JAM Past Year Papers and Model Test Paper (All Branches) - Math - 2019 Past Year Paper
Let a1 = b1 = 0, and for each n ≥ 2, let an and bn be real numbers given by
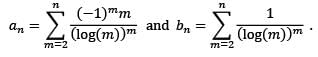
Then which one of the following is TRUE about the sequences {an} and {bn}?
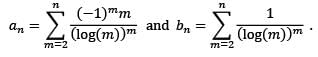
Let  Let V be the subspace of
Let V be the subspace of 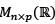 defined by
defined by
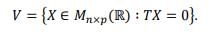
Then the dimension of V is
 Let V be the subspace of
Let V be the subspace of 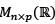 defined by
defined by 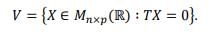
Let 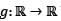 be a twice differentiable function. Define
be a twice differentiable function. Define 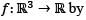
f(x,y,z) = g(x2 + y2 - 2z2).
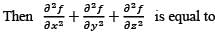
 be a twice differentiable function. Define
be a twice differentiable function. Define 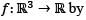
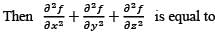
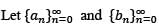 be sequences of positive real numbers such that nan < bn < n2an for
be sequences of positive real numbers such that nan < bn < n2an for
all n > 2. If the radius of convergence of the power series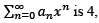 then the power series
then the power series
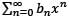
Let S be the set of all limit points of the set 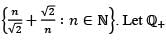 be the set of all positive
be the set of all positive
rational numbers. Then
If xhyk is an integrating factor of the differential equation y(1 + xy) dx + x(1 — xy) dy = 0, then the ordered pair (h, k) is equal to
If y(x) = λe2x + eβx, β ≠ 2, is a solution of the differential equation
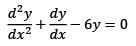
satisfying dy/dx (0) = 5, then y(0) is equal to
The equation of the tangent plane to the surface 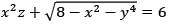 at the point (2, 0, 1) is
at the point (2, 0, 1) is
The area of the surface generated by rotating the curve x = y3, 0 ≤ y ≤ 1, about the y-axis, is
Let H and K be subgroups of 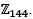 If the order of H is 24 and the order of K is 36, then the order of the subgroup H ∩ K is
If the order of H is 24 and the order of K is 36, then the order of the subgroup H ∩ K is
Let P be a 4 × 4 matrix with entries from the set of rational numbers. If 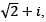 with
with  is a root of the characteristic polynomial of P and I is the 4 × 4 identity matrix, then
is a root of the characteristic polynomial of P and I is the 4 × 4 identity matrix, then
Let 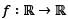 be a differentiable function such that f'(x) > f(x) for all
be a differentiable function such that f'(x) > f(x) for all 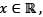 and f(0) = 1. Then f( 1) lies in the interval
and f(0) = 1. Then f( 1) lies in the interval
For which one of the following values of k, the equation 2x3 + 3x2 − 12x − k = 0 has three distinct real roots?
Let S be the family of orthogonal trajectories of the family of curves 2x2 + y2 = k, for 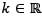 and k > 0. If
and k > 0. If 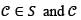 passes through the point (1, 2), then
passes through the point (1, 2), then 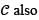 passes through
passes through
Let x, x + ex and 1 + x + ex be solutions of a linear second order ordinary differential equation with constant coefficients. If y(x) is the solution of the same equation satisfying y(0) = 3 and y'(0) = 4, then y(1) is equal to
The function f(x,y) = x3 + 2xy + y3 has a saddle point at
The area of the part of the surface of the paraboloid x2 + y2 + z = 8 lying inside the cylinder x2 + y2 = 4 is
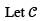 be the circle (x − 1)2 + y2 = 1, oriented counterclockwise. Then the value of the line integral
be the circle (x − 1)2 + y2 = 1, oriented counterclockwise. Then the value of the line integral
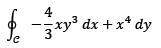 is
is
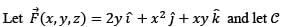 be the curve of intersection of the plane x + y + z = 1 and the cylinder x2 + y2 = 1. Then the value of
be the curve of intersection of the plane x + y + z = 1 and the cylinder x2 + y2 = 1. Then the value of
 is
is
The tangent line to the curve of intersection of the surface x2 + y2 − z = 0 and the plane x + y = 3 at the point (1, 1, 2) passes through
The set of eigenvalues of which one of the following matrices is NOT equal to the set of eigenvalues of 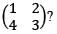
Let {an} be a sequence of positive real numbers such that a1 = 1, 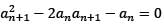 for all n ≥ 1.
for all n ≥ 1.
Then the sum of the series 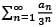 lies in the interval
lies in the interval
Let {an} be a sequence of positive real numbers. The series 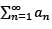 converges if the series
converges if the series
|
29 docs|48 tests
|
|
29 docs|48 tests
|




 is
is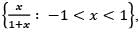 as a subset of
as a subset of 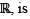
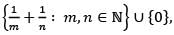 as a subset of
as a subset of 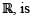
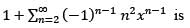




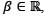 , define
, define 

















