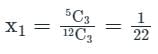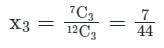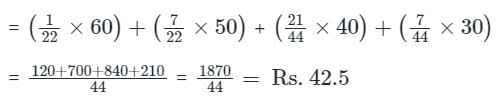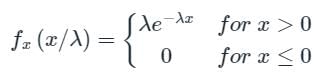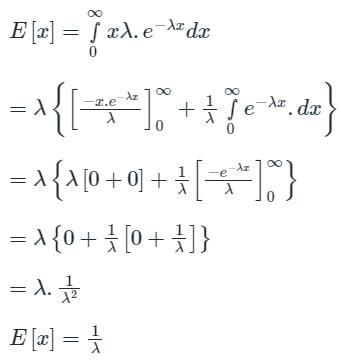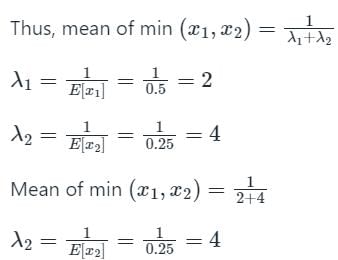Test: Poisson Distribution - Engineering Mathematics MCQ
10 Questions MCQ Test Engineering Mathematics - Test: Poisson Distribution
Let the probability density function of a random variable x be given as
f(x) = ae-2|x|
The value of ‘a’ is __________.
If X is a random variable with Mean μ, then the variance of X, denoted by Var (X) is given by:
Suppose the probability that a coin toss shows "head" is p, where 0 < p < 1. The coin is tossed repeatedly until the first "head" appears. The expected number of tosses required is
A discrete random variable X has the probability functions as:
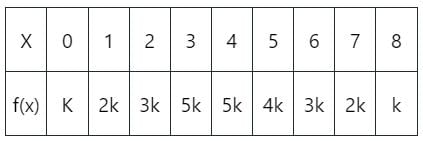
The value of E(X) is:
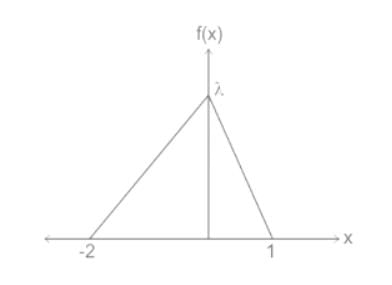
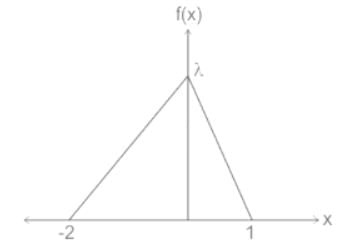
The graph of the probability density function of a random variable X is shown below. What should be the value of λ for this probability density function to be valid?
Given a PDF of a random variable X is:
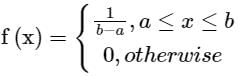
If a = -1 and b = 2, then for c = ½, P(|x| ≤ c) =
A man draws 3 balls from a jug containing 5 white balls and 7 black balls. He gets Rs. 20 for each white ball and Rs. 10 for each black ball. What is his expectation?
Let X1 and X2 be two independent exponentially distributed random variables with means 0.5 and 0.25, respectively. Then Y = min (X1, X2) is
If X is a Poisson variate with P(X = 0) = 0.6, then the variance of X is:
|
65 videos|133 docs|94 tests
|


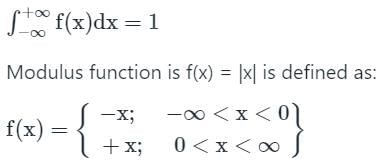
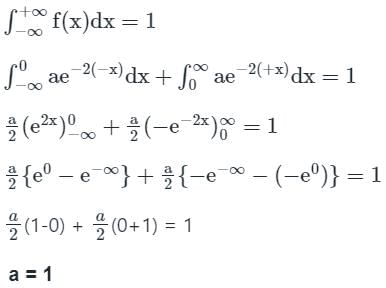
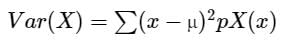


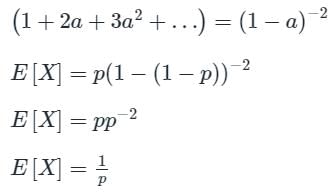

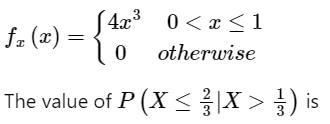
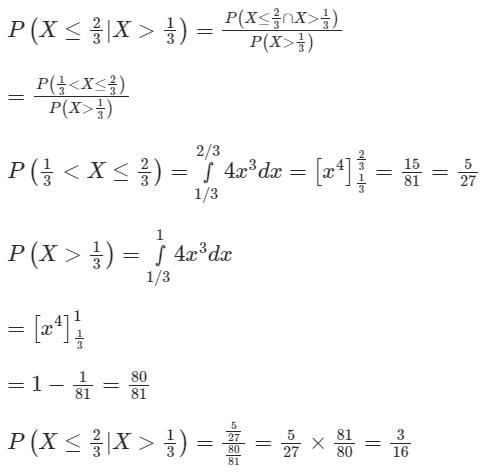
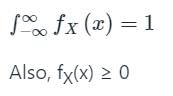
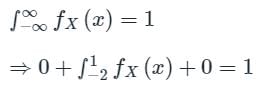
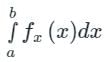
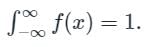 .
.