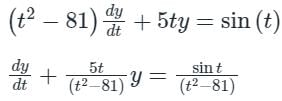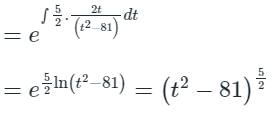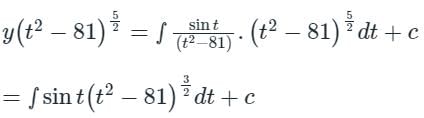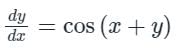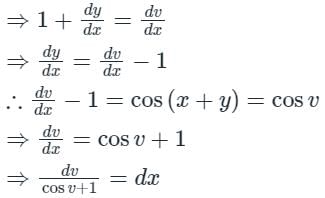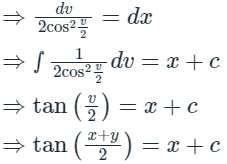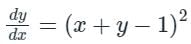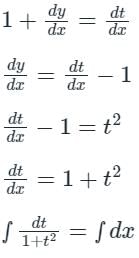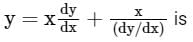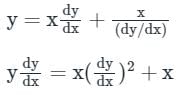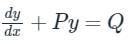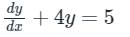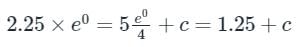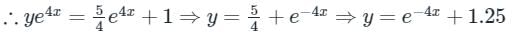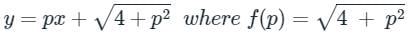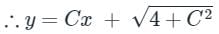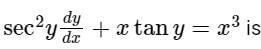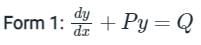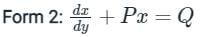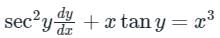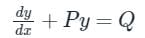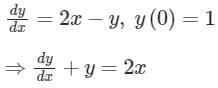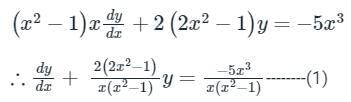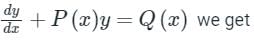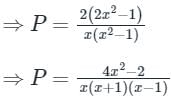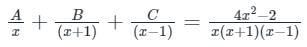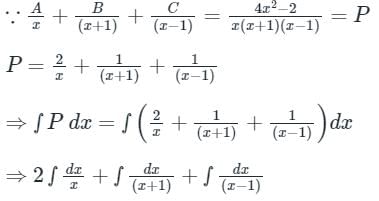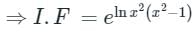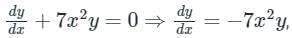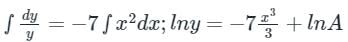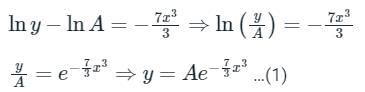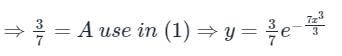Test: First Order Differential Equations - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Engineering Mathematics - Test: First Order Differential Equations - 2
Consider the differential equation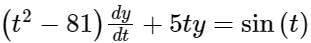 with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
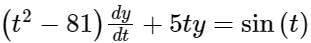 with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the intervalThe general solution of the differential equation dy/dx = cos(x + y), with c as a constant, is
Which one of the following is the general solution of the first order differential equation dy/dx = (x + y − 1)2, where x, y are real?
The differential equation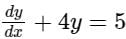 is valid in the domain 0 ≤ x ≤ 1 with y (0) = 2.25 The solution of the differential equation is
is valid in the domain 0 ≤ x ≤ 1 with y (0) = 2.25 The solution of the differential equation is
The solution of the differential equation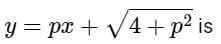
Consider the initial value problem below. The value of y at x = In 2, (rounded off to 3 decimal places) is dy/dx = 2x - y, y(0) = 1 (Important - Enter only the numerical value in the answer)
The integrating factor of the differential equation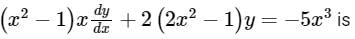
For the equation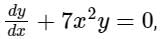 if y(0) = 3/7, then the value of y(1) is
if y(0) = 3/7, then the value of y(1) is
|
65 videos|122 docs|94 tests
|