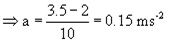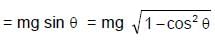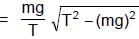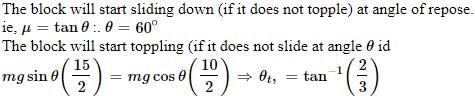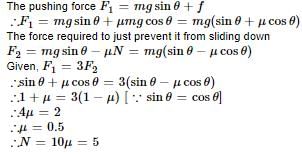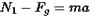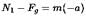Test: Newton’s Second Law of Motion - NEET MCQ
11 Questions MCQ Test Topic-wise MCQ Tests for NEET - Test: Newton’s Second Law of Motion
A constant force acting on a body of mass 3 kg changes its speed from 2 m/s to 3.5 m/s in 10 second. If the direction of motion of the body remains unchanged, what is the magnitude and direction of the force?
A simple pendulum is oscillating in a vertical plane. If resultant acceleration of bob of mass m at a point A is in horizontal direction, find the tangential force at this point in terms of tension T and mg.
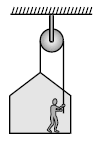
A painter is applying force himself to raise him and the box with an cceleration of 5 m/s2 by a massless rope and pulley arrangement as shown in figure. Mass of painter is 100 kg and that of box is 50 kg. If g = 10 m/s2, then :
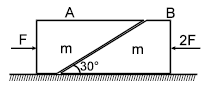
Two blocks ‘A’ and ‘B’ each of mass ‘m’ are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on the two blocks ‘A’ and ‘B’ respectively as shown in figure. The block A does not slide on block B. Then the normal reaction acting between the two blocks is :
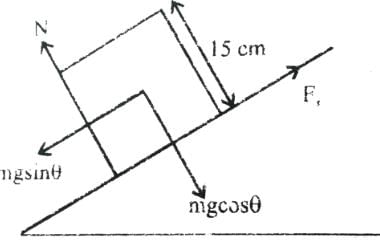
A block of base 10 cm × 10 cm and height 15 cm is kept on an inclined plane. The coefficient of friction between them is . The inclination q of this inclined plane from the horizontal plane is gradually increased from 0º. Then [jee 2009]
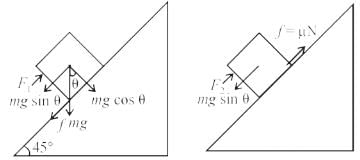
A block is moving on an inclined plane making an angle 45º with horizontal and the coefficient of friciton is μ. the force required to just push it up the inclined plane is 3 times the force requried to just prevent it from sliding down. If we define N = 10μ, then N is
[jee 2011]
The dimensional formula of Plancks’s constant and angular momentum are
Three forces 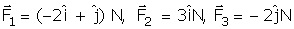 act on an object of mass m = 2 kg. The acceleration of the object in m/s2 is:
act on an object of mass m = 2 kg. The acceleration of the object in m/s2 is:
Upon catching a ball, a cricket fielder swings his hands backwards. The concept behind this is explained by
The mass of a lift is 2000 kg. When the tension in the supporting cable is 28000 N, its acceleration is:
If a lift is moving with constant acceleration 'a' in the upward direction, then the force applied by mass m on the floor of the lift will be:
|
9 docs|806 tests
|