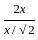NDA Mock Test: Mathematics - 9 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2025 - NDA Mock Test: Mathematics - 9
What is the largest power of 10 that divides the product 29 × 28 × 27 × ...2 × 1 ?
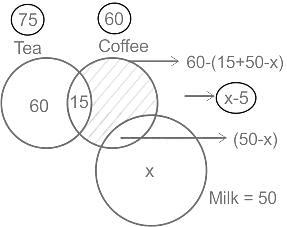
In a party of 150 persons, 75 persons take tea, 60 persons take coffee and 50 persons take milk. 15 of them take both tea and coffee, but no one taking milk takes tea. If each person in the party takes at least one drink, then what is the number of persons taking milk only ?
It is given that 5 does not divide n - 1, n and n + 1, where n is a positive integer. Which one of the following is correct ?
If α and β are the roots of the equation x2 - 7x + 1 = 0, then what is the value of α4 + β4 ?
Consider the following statements in respect of all factors of 360 :
1. The number of factors is 24.
2. The sum of all factors is 1170.
Which of the above statements is/are correct ?
There are four bells which ring at an interval of 15 minutes, 25 minutes, 35 minutes and 45 minutes respectively. If all of them ring at 9 A.M., how many more times will they ring together in the next 72 hours ?
Consider the following statements :
1. n3 - n is divisible by 6.
2. n5 - n is divisible by 5.
3. n5 - 5n3 + 4n is divisible by 120.
Which of the statements given above are correct ?
Consider the following statements in respect of the polynomial 1 - x - xn + xn+1 where n is a natural number :
1. It is divisible by 1 - 2x + x2.
2. It is divisible by 1 - xn.
Which of the statements given above is/are correct ?
If 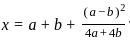 and
and 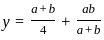 then what is the value of (x - a)2 - (y - b)2 ?
then what is the value of (x - a)2 - (y - b)2 ?
If tan8 θ + cot8 θ = m, then what is the value of tan θ + cot θ ?
What is the value of x that satisfies 4 cos2 30° + 2x sin 30° - cot2 30° - 6 tan 15° tan 75° = 0 ?
Let ABC be a right-angled triangle with sides 5 cm, 12 cm and 13 cm. If p is the length of the perpendicular drawn from vertex A on the hypotenuse BC, then what is the value of 13p ?
The surface area of a cube is increased by 25%. If p is the percentage increase in its length, then which one of the following is correct ?
The length of a diagonal of a cuboid is 11 cm. The surface area is 240 square cm. What is the sum of its length, breadth and height ?
A floor of a big hall has dimensions 30 m 60 cm and 23 m 40 cm. It is to be paved with square tiles of same size. What is the minimum number of tiles required ?
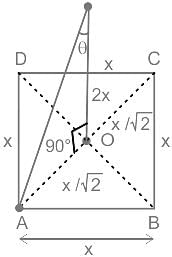
ABCD is a square field with AB = x. A vertical pole OP of height 2x stands at the centre O of the square field. If ∠APO = θ, then what is cot θ equal to ?
Item contains a Question followed by two Statements. Answer each item using the following instructions :
A number 277XY5 (where X, Y are digits) is divisible by 25.
Question: What is the value of X ?
Statement I: The given number is divisible by 9.
Statement II: X > 5.
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: What are the unique values of a, b and c if 2 is a root of the equation ax2 + bx + c = 0 ?
Statement I: Ratio of c to a is 1.
Statement II: Ratio of b to a is (-5/2).
Item contains a Question followed by two Statements. Answer each item using the following instructions :
Question: Is p2 + q2 + q odd, where p, q are positive integers ?
Statement I: 2p + q is odd.
Statement II: q - 2p is odd.
|
2 docs|101 tests
|



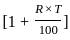
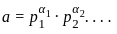
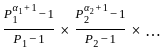
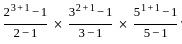
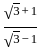 and y =
and y = 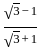 then what is the value x3 - y3 ?
then what is the value x3 - y3 ?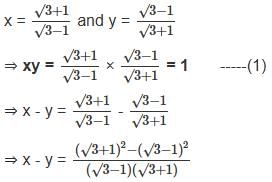
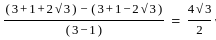
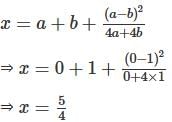
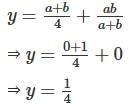
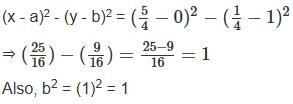
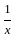 )2 = (x2 +
)2 = (x2 + 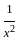 ) + 2
) + 2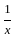
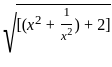
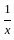
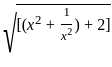
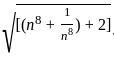
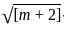
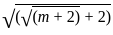

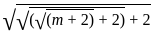


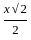 =
= 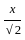
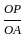 =
=