Test: Analytic Functions - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Analytic Functions - 1
A function f of the complex variable z = x + i y, is given as f(x, y) = u(x, y) + i v(x, y), where u(x, y) = 2kxy and v(x, y) = x2 – y2. The value of k, for which the function is analytic is _____
The function f(z) of complex variable z = x + iy, where i = √−1, is given as f(z) = (x3 – 3xy2) + i v(x,y). For this function to be analytic, v(x,y) should be
If f(z) = u + iv is an analytic function of z = x + iy and u – v = ex (cosy - siny), then f(z) in terms of z is
If f (z) is an analytic function whose modulus is constant, then f (z) is a
The Cauchy Riemann equations for f(z) = u(x, y) + iv(x, y) to be analytic are:
If f(z) is an analytic function whose real part is constant then f(z) is
Let f(Z) = u(x, y) + i(v(x, y)) be an analytical function. If u = 5x + 2xy then v is equal to _________, where c is a constant.
Which of the following function f(z), of the complex variable z, is NOT analytic at all the points of the complex plane?


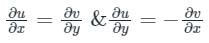
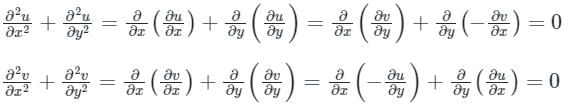
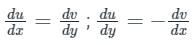
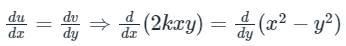 2ky = -2y ⇒ k = -1
2ky = -2y ⇒ k = -1
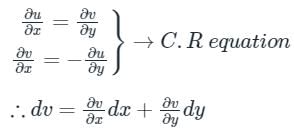
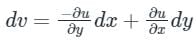
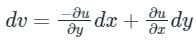 (This is an exact differential equation)
(This is an exact differential equation)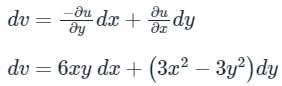
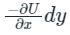
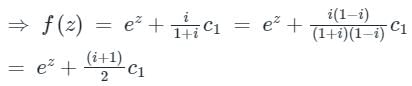
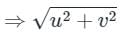 = k ⇒ u2 + v2 = k
= k ⇒ u2 + v2 = k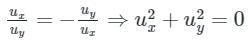
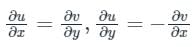
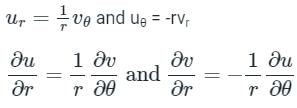
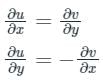
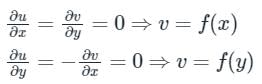

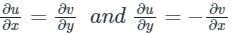
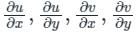 are continuous function of x and y.
are continuous function of x and y.