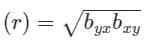Test: Regression Analysis - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Regression Analysis
Consider the following learning algorithms:
(a) Logistic regression
(b) Back propagation
(c) Linear repression
Which of the following option represents classification algorithms?
For a bivariate data set on (x, y), if the means, standard deviations and correlation coefficient are
x̅ = 1.0, y̅ = 2.0, sx = 3.0, sy = 9.0, r = 0.8
Then the regression line of y on x is:
x̅ = 1.0, y̅ = 2.0, sx = 3.0, sy = 9.0, r = 0.8
Then the regression line of y on x is:
If a constant 60 is subtracted from each of the values of X and Y, then the regression coefficient is
The data about the sales and advertisement expenditure of a firm is given below

The correlation coefficient between sales and advertisement expenditure is 0.9. The likely sales for a proposed advertisement expenditure of Rs. 10 crore
In Regression Analysis, if a quantitative variable has 'm' categories, one can introduce
Dimension reduction methods have the goal of using the correlation structure among the predictor variables to accomplish which of the following:
A. To reduce the number of predictor components
B. To help ensure that these components are dependent
C. To provide a framework for interpretability of the results
D. To help ensure that these components are independent
E. To increase the number of predictor components
Choose the correct answer from the options given below:
Given the regression lines X + 2Y - 5 = 0, 2X + 3Y - 8 = 0 and Var(X) = 12, the value of Var(Y) is
For the regression equations
y = 0.516x + 33.73
and
x = 0.512 y + 32.52
the means of x and y are nearly
If x and y are uncorrelated variables then this implies:
If the two regression lines are as under :
Y = a + bX
X = c + dY
What is the correlation coefficient between variables X and Y?



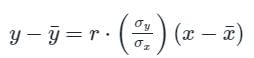
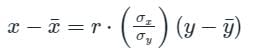
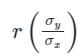 is called the regression co-efficient of y on x and is denoted by byx
is called the regression co-efficient of y on x and is denoted by byx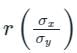 is called the regression co-efficient of x on y and is denoted by bxy
is called the regression co-efficient of x on y and is denoted by bxy