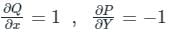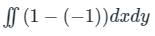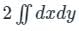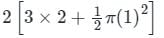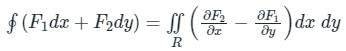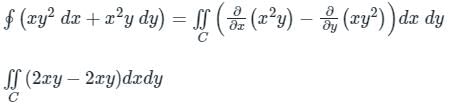Test: Green's Theorem - Engineering Mathematics MCQ
10 Questions MCQ Test - Test: Green's Theorem
The value of 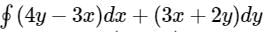 where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
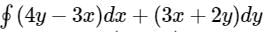 where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.Using Green’s theorem, the value of the integral 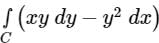 , where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
, where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
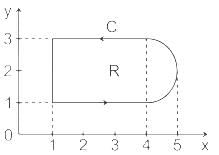
Consider the line integral ∫c(xdy − ydx) the integral being taken in a counter clockwise direction over the closed curve C that forms the boundary of the region R shown in the figure below. The region R is the area enclosed by the union of a 2 × 3 rectangle and a semi-circle of radius 1. The line integral evaluates to
Suppose C is the closed curve defined as the circle x2 + y2 = 1 with C oriented anti-clockwise. The value of ∮(xy2dx + x2ydy) over the curve C equals ________
The Green’s theorem can be related to which of the following theorems mathematically?


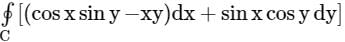 where C is the circle x2 + y2 = 1, is:
where C is the circle x2 + y2 = 1, is: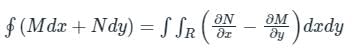
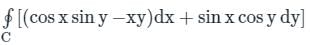
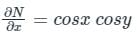
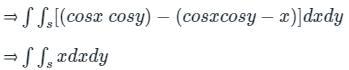
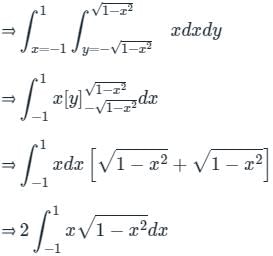
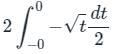
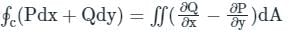
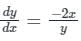
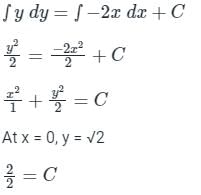
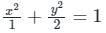
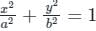 we get:
we get:
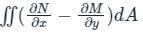
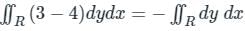
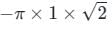
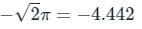

 then
then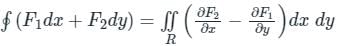
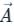 around a (closed) path L is
around a (closed) path L is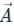 over the open surface S bounded by L
over the open surface S bounded by L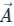 are continuous on S.
are continuous on S.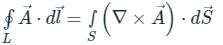
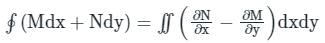
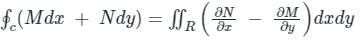
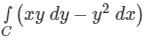
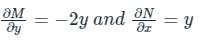
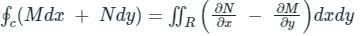
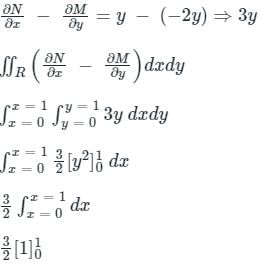
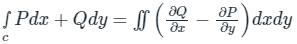
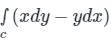 , i.e
, i.e