Test: Extended Transition Function - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Extended Transition Function
The number of tuples in an extended Non Deterministic Finite Automaton:
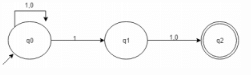
Choose the correct option for the given statement:Statement: The DFA shown represents all strings which has 1 at second last position
. 
What is wrong in the given definition?Def: ({q0, q1, q2}, {0,1}, δ, q3, {q3})
If δ is the transition function for a given NFA, then we define the δ’ for the DFA accepting the same language would be:Note: S is a subset of Q and a is a symbol.
What is the relation between DFA and NFA on the basis of computational power?
If a string S is accepted by a finite state automaton, S=s1s2s3……sn where siϵ∑ and there exists a sequence of states r0, r1, r2…… rn such that δ(r(i), si+1) =ri+1 for each 0, 1, …n-1, then r(n) is:
According to the given table, compute the number of transitions with 1 as its symbol but not 0:
Number of times the state q3 or q2 is being a part of extended 6 transition state is
Predict the missing procedure:
1.Δ(Q0, ε) ={Q0},
2.Δ(Q0, 01) = {Q0, Q1}
3.δ(Q0, 010) =?



















