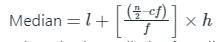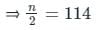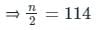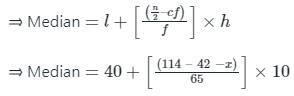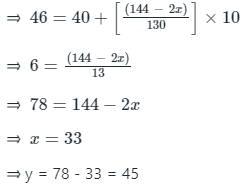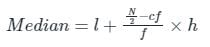परीक्षा: केंद्रीय प्रवृत्तियों के माप - 1 - SSC CGL MCQ
10 Questions MCQ Test - परीक्षा: केंद्रीय प्रवृत्तियों के माप - 1
संख्याओं 10, 8, 2, 7, 3, 8, 5, 1 का माध्यिका k है। यदि 10 को 1 से बदल दिया जाए, तो नई माध्यिका r है। (k - r) का मान क्या है?
मान लें कि x, y, z तीन अवलोकन हैं। इन अवलोकनों का माध्य है
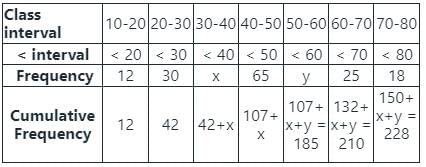
निम्नलिखित वितरण में, माध्यिका का मान 46 है, और x + y = 78, तब x और y के मान हैं:

यदि 14, 13, 18, 16, k, (k + 3) का औसत 13 है, तो k, 8, 9, 11, 5, 10, 6 का औसत क्या होगा?
8, 5, 7, 10, 15, 21, 5, 7, 2, 5 का मोड क्या है?
संचयी आवृत्ति तालिका का निर्माण किसके निर्धारण में सहायक होता है?
यदि 10 संख्याओं का औसत 96 है और इनमें से एक संख्या 150 है, तो शेष नौ संख्याओं का औसत क्या होगा?
नीचे छात्रों के एक परीक्षा के परिणाम दिए गए हैं। दिए गए परिणामों का मोड खोजें।
90, 80, 77, 86, 90, 91, 77, 25, 45, 35, 66, 69, 65, 43, 65, 75, 43, 90, 89।
4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6 की माध्यिका ज्ञात करें।