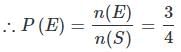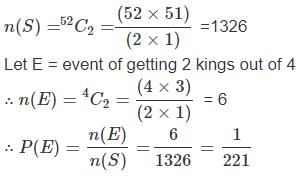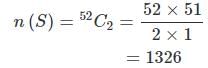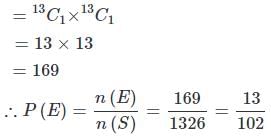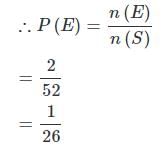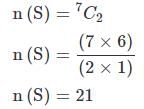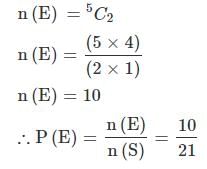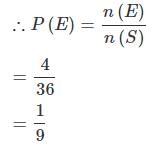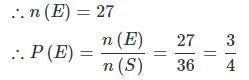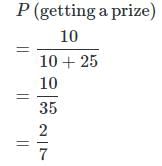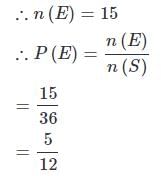परीक्षा: संभावना सिद्धांत - 1 - SSC CGL MCQ
10 Questions MCQ Test - परीक्षा: संभावना सिद्धांत - 1
दो सिक्कों के एक साथ उछालने पर कम से कम एक सिरा आने की संभावना है-
52 पत्तों के एक पैक से, दो पत्ते एक साथ बेतरतीब ढंग से खींचे जाते हैं। दोनों पत्तों का राजा होने की संभावना क्या है?
एक थैले में 6 काले और 8 सफेद गेंदें हैं। एक गेंद को यादृच्छिक रूप से निकाला जाता है। निकाली गई गेंद के सफेद होने की संभावना क्या है?
52 पत्तों के एक पैक से एक साथ दो पत्ते निकाले जाते हैं। यह संभावना कि एक पत्ता स्पेड है और दूसरा हार्ट है, है:
52 पत्तों के एक पैक से एक पत्ता निकाला जाता है। क्लब की रानी या दिल के राजा पाने की संभावना क्या है?
एक थैले में 2 लाल, 3 हरे और 2 नीले गेंदें हैं। दो गेंदें यादृच्छिक रूप से निकाली जाती हैं। यह संभावना क्या है कि निकाली गई गेंदों में से कोई भी नीली नहीं है?
दो पासों के फेंकने पर 9 का योग प्राप्त करने की संभावना क्या है?
दो पासे एक साथ फेंके जाते हैं। उन दो संख्याओं का गुणनफल सम आने की संभावना क्या है?
एक लॉटरी में 10 पुरस्कार और 25 रिक्त स्थान हैं। एक लॉटरी को यादृच्छिक रूप से निकाला जाता है। पुरस्कार पाने की संभावना क्या है?
दो पासे फेंके जाते हैं। कुल स्कोर का एक प्रमुख संख्या होने की संभावना है: