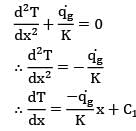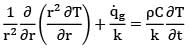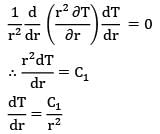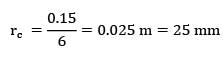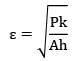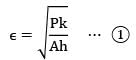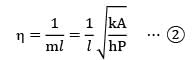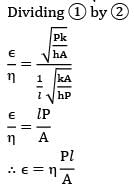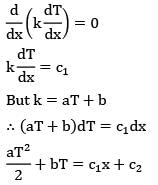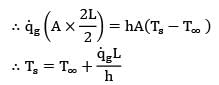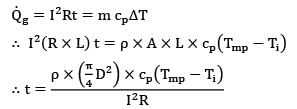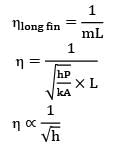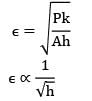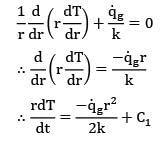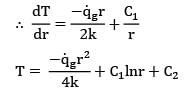Test: Conduction Level - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test Heat Transfer - Test: Conduction Level - 1
The general heat conduction equation for 1D heat flow is given as
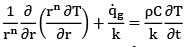
For Cartesian coordinates, n is equal to
What is the total number of known conditions required to get a particular solution of a 3D unsteady state heat conduction problem
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following options does not follow lumped system analysis during heat or cooling process
An iron block gets heated up or cools down very fast as compared to water because of __________.
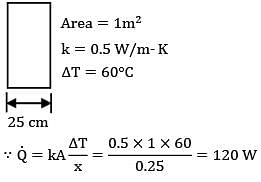
A plane wall is 25 cm thick with an area of 1 m2 and has a thermal conductivity of 0.5 W/m-K. If a temperature difference of 60°C is imposed across it, what is the heat transfer rate?
For steady state 1D heat conduction through a planar wall with internal heat generation, the temperature profile is
What is the expression for resistance against thermal conduction through a hollow sphere of inner radius r1 and outer radius r2, and thermal conductivity k?
Consider radial steady state heat conduction through a hollow spherical conductor carrying a heat source inside the sphere. The temperature distribution in the shell T = T (r ) is __________
T is the temperature at a distance r from the center.
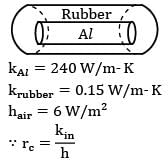
An electric cable of aluminium conductor (k = 240 W/m-K) is to be insulated with rubber (k = 0.15 W/m-K). The cable is exposed to air (h = 6 W/m2-K). The critical radius of insulation will be
Which of the following statements is true regarding fins (extended surfaces for enhanced heat dissipation from a surface)?
The figure below shows a cross section of an insulated heating pipe which is made from steel (k = 45 W/m-K) with an inner radius of 150 mm and outer radius of 155 mm. The pipe is coated with 100 mm thickness of insulation having thermal conductivity of k = 0.006 W/m-K.Air at a temperature Ti = 60°C flows through the pipe. The value of corresponding convective coefficient is hi = 35 W/m2-K. The outside surface of the pipe is exposed to air which is 15°C at and convective heat transfer coefficient on this surface has a value of ho = 10 W/m2-K. Find the critical radius of insulation.
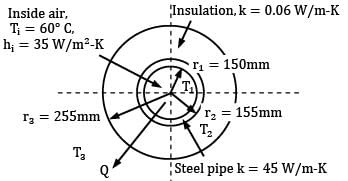
Surrounding air T0 = 15°C,ho = 10W/m2-K
The fin efficiency is defined as the ratio of the actual heat transfer from the fin to
A hot surface at 80°C exposed to air at 20°C is to be cooled by attaching 10-cm-long and 1-cm-diameter cylinder fins. The combined heat transfer coefficient is 30 W/m2 . K, and heat transfer from the fin tip is negligible. If the fin efficiency is 0.75, the rate of heat loss from 100 fins is
The effectiveness (∊) and efficiency (?) of a fin (extended surfaces) can be related as
Consider a very hot small size copper ball dropped in cold water. The temperature of the ball drops down __________ with time.
The thermal conductivity of a solid depends upon the solid’s temperature as k = aT = + b where a and b are constants. The temperature in a planar layer of this solid as it conducts heat is given by
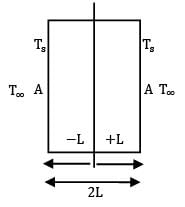
A plane wall of thickness 2L has a uniform volumetric heat source![]() It is exposed to local ambient temperature T∞ at both the ends (x = ±L). The surface temperature Tg of the wall under steady-state condition (where h and k have their usual meanings) is given by
It is exposed to local ambient temperature T∞ at both the ends (x = ±L). The surface temperature Tg of the wall under steady-state condition (where h and k have their usual meanings) is given by
A very thin water jacketed copper rod ‘D’ m in diameter is used to carry current. The cooling water which flows continuously in the jacket, maintains the rod temperature at Ti°C during normal operation at ‘I’ amps. The electrical resistance of the rod is known to be R ?/m . If the coolant water ceased to be available and the heat removal rate diminished greatly, the rod would eventually melt. What is the time required for melting to start if the melting point of the rod material is Tmp? (cp is the specific heat and ρ is the density of the rod material.)
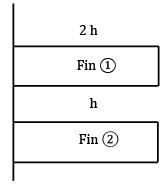
Two finned surfaces with long fins are identical, except that the convection heat transfer coefficient for the first finned surface is twice that of the second one. What statement below is accurate for the efficiency and effectiveness of the first finned surface relative to the second one?
The radial variation of temperature in an electrical wire carrying current is __________.
|
57 videos|77 docs|86 tests
|
|
57 videos|77 docs|86 tests
|