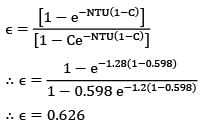Test: Heat Exchanger Level - 2 - Mechanical Engineering MCQ
10 Questions MCQ Test Heat Transfer - Test: Heat Exchanger Level - 2
In a counter flow heat exchanger, the working parameters for hot fluid are as follows: heat capacity = 2 kJ/kg K, mass flow inlet temperature 150oC , outlet temperature 100oC. For the cold fluid, the parameters are: heat capacity = 4 kJ/kg K, - mass flow rate 10 kg/s, and inlet temperature is = 20oC. The outlet temperature of the cold fluid in oC is
Cold water at 10oC enters a counter flow heat exchanger at a rate of 8 kg/s , where it is heated by a hot water that enters the heat exchanger at 70oC and flows at a rate of 2kh/s . Assume specific heat of water to be cp = 4.18 kJ/kgoC . Determine the maximum theoretical heat transfer rate?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cross flow type air heater has an area of 50 m2. The overall transfer coefficient 100 W/m2 -and heat capacity of both hot and cold streams is 1000 W/K. The value of NTU is
The overall heat transfer coefficient for a shell and tube heat exchanger for clean surfaces is Uo = 400 W/m2- K. The fouling factor after one year of operation is found to be hfo = 200 W/m2 -K. The overall heat transfer coefficient at this time is
In a solar assisted air conditioning system, 1 kg/sec of ambient air is to be preheated by the same amount of air leaving the system. A counter-flow heat exchanger having an area of 60m2 with overall heat transfer coefficient of 25 W/m2 - K is used for this purpose. Assuming for air is 1kJ/kg K. The effectiveness of the heat exchanger is
In a double-pipe heat exchanger, the cold fluid is water with inlet temperature of 20oC and mass flow rate of 20 kg/s and the hot fluid which also has water inlet temperature of 80oC and mass flow rate of 10 kg/s. For water cp = 4.2kj/kg oC.
. What is the maximum temperature to which the cold fluid can be heated in a parallel flow and in a counter flow heat exchanger?
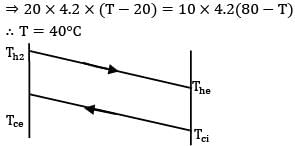
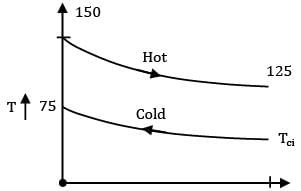
In a double-pipe counter flow heat exchanger 1000kh/h, oil having a specific heat 20 j/kg -K is cooled from 150oC to 125oC by 1250 kg/h of fluid having specific heat 16j/kg-K. The cold fluid leaves the heat exchanger at 75oC . In this case, the temperature at which the cooling fluid enters the heat exchanger and LMTD are __________
A counter flow shell and tube type heat exchanger is used to heat water with hot exhaust gases. The water (c = 4180 j/kg-K ) flows at the rate of 2 kg/s and the exhaust gases (c = 1000 j/kg - K) flow at the rate of 5 kg/s. If the heat transfer surface area is 32 m2 and the overall heat transfer coefficient is 200 W/m2 -K , the effectiveness of the heat exchanger is __________.
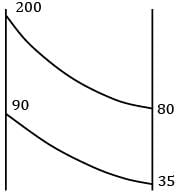
In a counterflow heat exchanger, hot gases enter the system at 200°C and leave at 80°C. the temperature of the outside air entering the unit is 35°C. Its temperature at the exit 90°C. the heat exchanger has an effectiveness of
A counter flow shell and tube heat exchanger is used to heat water with hot exhaust gases. The water (C = 4180 J/kg K) flows at the rate of 2 kg/s and the exhaust gases (c = 1000 J/kg K) flow at the rate of 5 kg/s. If the heat transfer surface area is 32 m2 and the overall heat transfer coefficient is 200 W/m2K, the NTU of the heat exchanger i
|
57 videos|77 docs|86 tests
|
|
57 videos|77 docs|86 tests
|
Top Courses for Mechanical Engineering
Important Questions for Heat Exchanger Level - 2
Heat Exchanger Level - 2 MCQs with Answers
Online Tests for Heat Exchanger Level - 2 Heat Transfer
|
© EduRev
|
Education Revolution
|
Follow Us
|
