Explore Exams
Login Signup
Sign in Open App
Class 10 Exam  >  Class 10 Tests  >  Measures of Central Tendency - Mean, Median and Mode - Class 10 MCQ

Measures of Central Tendency - Mean, Median and Mode - Class 10 MCQ


Test Description

15 Questions MCQ Test - Measures of Central Tendency - Mean, Median and Mode

Measures of Central Tendency - Mean, Median and Mode for Class 10 2025 is part of Class 10 preparation. The Measures of Central Tendency - Mean, Median and Mode questions and answers have been prepared according to the Class 10 exam syllabus.The Measures of Central Tendency - Mean, Median and Mode MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Measures of Central Tendency - Mean, Median and Mode below.
Solutions of Measures of Central Tendency - Mean, Median and Mode questions in English are available as part of our course for Class 10 & Measures of Central Tendency - Mean, Median and Mode solutions in Hindi for Class 10 course. Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Attempt Measures of Central Tendency - Mean, Median and Mode | 15 questions in 15 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
Measures of Central Tendency - Mean, Median and Mode - Question 1
Save

The marks of 6 students are: 12, 15, 17, 20, 22, 25. Find the median.

Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 1

n = 6 (even).
Median = [(n/2)th term + ((n/2)+1)th term] ÷ 2.
(6/2)th term = 3rd term = 17.
(6/2 + 1)th = 4th term = 20.
Median = (17 + 20) ÷ 2 = 18.5.
Hence Option B is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 2
Save

The marks of 5 students are: 10, 15, 20, 25, 30. Find the arithmetic mean.

Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 2

Formula: Mean = (Σx) ÷ n.
Σx = 10 + 15 + 20 + 25 + 30 = 100.
n = 5.
Mean = 100 ÷ 5 = 20.
Hence Option A is correct.

Clear all your doubts with EduRev
Measures of Central Tendency - Mean, Median and Mode - Question 3
Save

Find the mean of first 5 natural numbers.

Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 3

Numbers are 1, 2, 3, 4, 5.
Σx = 1 + 2 + 3 + 4 + 5 = 15.
n = 5.
Mean = 15 ÷ 5 = 3.
Hence Option C is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 4
Save

The ages of 7 students are: 10, 12, 13, 14, 15, 16, 20. Find the median age.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 4

n = 7 (odd). Median = (n+1)/2 th term = 4th term. 4th term = 14. Hence median = 14. Option B is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 5
Save

The weights (in kg) of 5 persons are 67, 65, 71, 57, and 45. What is the arithmetic mean of their weights?
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 5

Step 1: Sum of weights Σx = 67 + 65 + 71 + 57 + 45 = 305 kg.
Step 2: Number of persons n = 5.
Step 3: Mean = Σx / n = 305 / 5 = 61 kg.
Conclusion: The arithmetic mean is 61 kg, making Option C correct.

Measures of Central Tendency - Mean, Median and Mode - Question 6
Save

The marks of 7 students are 40, 45, 50, 55, 60, 65, 70. What is the median?
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 6

Step 1: Arrange in order: 40, 45, 50, 55, 60, 65, 70 (already ordered).
Step 2: n = 7 (odd), median at (7+1)/2 = 4th term.
Step 3: 4th term = 55.
Conclusion: The median is 55, So Option B correct.

Measures of Central Tendency - Mean, Median and Mode - Question 7
Save

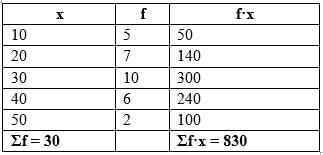
For the grouped data below, what is the mean using direct method?
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 7

Step 1: Calculate fx: 5 × 4 = 20, 15 × 6 = 90, 25 × 8 = 200, 35 × 2 = 70.
Step 2: Σfx = 20 + 90 + 200 + 70 = 380, Σf = 4 + 6 + 8 + 2 = 20.
Step 3: Mean = Σfx / Σf = 380 / 20 = 19.

Measures of Central Tendency - Mean, Median and Mode - Question 8
Save

The daily wages of 6 workers are: 120, 150, 160, 180, 200, 250. Find the median.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 8

n = 6 (even). Median = Average of (n/2)th term and ((n/2)+1)th term. (6/2)th term = 3rd term = 160. (6/2 + 1)th = 4th term = 180. Median = (160 + 180) ÷ 2 = 170. Hence Option B is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 9
Save

The marks obtained are: 12, 14, 18, 20, 20, 22, 25. Find the mode.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 9

Mode is the value occurring most frequently. Here 20 occurs twice, all others occur once. So Mode = 20. Hence Option A is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 10
Save

The frequency distribution is:

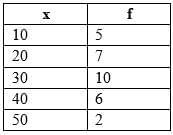
Find the mean.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 10

Mean = Σfx ÷ Σf.

= 830 ÷ 30 = 27.67 ≈ 28.

Hence Option A is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 11
Save

The ages of 9 students are: 8, 10, 12, 12, 13, 14, 14, 15, 16. Find the mode.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 11

Count frequencies:

  • 12 occurs 2 times.
  • 14 occurs 2 times.
  • Others occur once.

When there are two values with the same highest frequency, the data is bimodal.

Modes are 12 and 14. Since both appear in options, the higher (14) is chosen.

Hence Option C is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 12
Save

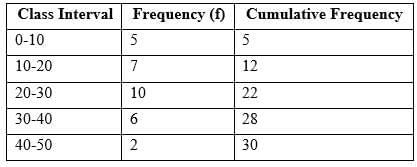
The following distribution is given:

Find the median class.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 12

Total frequency Σf = 5 + 7 + 10 + 6 + 2 = 30.

n/2 = 30/2 = 15.

Cumulative frequency table:

The 15th observation lies in 20-30.

So median class = 20-30.

Hence Option C is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 13
Save

The marks of 8 students are: 5, 7, 8, 10, 12, 12, 15, 18. Find the mean.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 13

Σx = 5+7+8+10+12+12+15+18 = 87.
n = 8.
Mean = 87 ÷ 8 = 10.875.
Hence Option A is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 14
Save

In a frequency distribution, the modal class is 20-30 with frequency 10. The preceding class has frequency 7 and succeeding class has frequency 6. Class width = 10. Find the mode.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 14

Formula: Mode = L + [(f₁ − f₀) ÷ (2f₁ − f₀ − f₂)] × h.
L = lower limit of modal class = 20.
f₁ = frequency of modal class = 10.
f₀ = frequency of preceding class = 7.
f₂ = frequency of succeeding class = 6.
h = 10.
Mode = 20 + [(10−7)/(20−7−6)] × 10.
= 20 + (3/7) × 10.
= 20 + 30/7 = 24.3.
Hence Option C is correct.

Measures of Central Tendency - Mean, Median and Mode - Question 15
Save

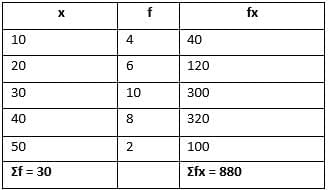
The following data shows marks of students:

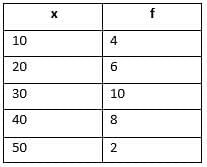
Find the mean marks.
Detailed Solution for Measures of Central Tendency - Mean, Median and Mode - Question 15

Mean = Σfx ÷ Σf.
= 880 ÷ 30 = 29.3.
Rounded = 29.
Hence Option B is correct.

Information about Measures of Central Tendency - Mean, Median and Mode Page
In this test you can find the Exam questions for Measures of Central Tendency - Mean, Median and Mode solved & explained in the simplest way possible. Besides giving Questions and answers for Measures of Central Tendency - Mean, Median and Mode, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Measures of Central Tendency - Mean, Median and Mode

Find all the important questions for Measures of Central Tendency - Mean, Median and Mode at EduRev.Get fully prepared for Measures of Central Tendency - Mean, Median and Mode with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Measures of Central Tendency - Mean, Median and Mode syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Measures of Central Tendency - Mean, Median and Mode resources.

Measures of Central Tendency - Mean, Median and Mode MCQs with Answers

Prepare for the Measures of Central Tendency - Mean, Median and Mode within the Class 10 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Measures of Central Tendency - Mean, Median and Mode

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Measures of Central Tendency - Mean, Median and Mode with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup