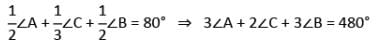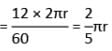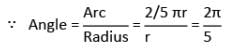MCQ: पूरक कोण - 2 - Bank Exams MCQ
15 Questions MCQ Test - MCQ: पूरक कोण - 2
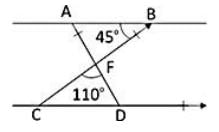
दी गई आकृति में, AB || CD, m∠ABF = 45° और m∠CFC = 110° है। तब, m∠FDC है:

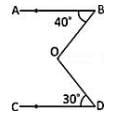
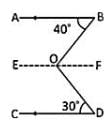
दी गई आकृति में, AB || CD, ∠ABO = 40° और ∠CDO = 30° है। यदि ∠DOB = x° है, तो x का मान क्या है?
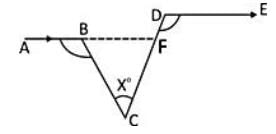
सन्निहित चित्र में, ∠ABC = 100°, ∠EDC = 120° और AB || DE है। तब, ∠BCD के मान के बराबर है:
त्रैपेज़ियम PQRS में, QR || PS, ∠Q = 90°, PQ = QR और ∠PRS = 20° है। यदि ∠TSR = θ है, तो θ का मान क्या होगा?: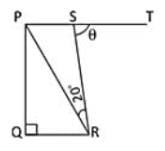
दिए गए चित्र में AB || CD, ∠A = 128°, ∠E = 144° है। तब, ∠FCD के मान के बराबर है:

दी गई आकृति में रेखाएँ AP और OQ बिंदु G पर मिलती हैं। यदि ∠AGO + ∠PGF = 70° और ∠PGQ = 40° है, तो ∠PGF का कोण मान ज्ञात करें।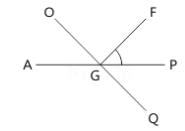
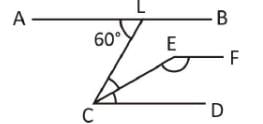
दी गई चित्र में AB || CD है, ∠ALC = 60° है और EC ∠LCD का बिसेक्टर है। यदि EF || AB है, तो ∠CEF का मान क्या होगा।
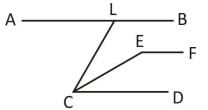
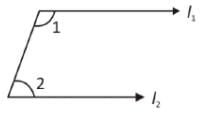
यदि एक कोण की भुजाएँ दूसरे कोण की भुजाओं के समानांतर हैं, तो दोनों कोण क्या होंगे?
एक पहिया प्रत्येक मिनट में 12 क्रांति करता है। एक सेकंड में पहिये के एक तीर द्वारा वर्णित कोण (रेडियन में) क्या होगा?
निम्नलिखित कथनों पर विचार करें:
I. उन बिंदुओं का स्थान जो दो समानांतर रेखाओं से समान दूरी पर हैं, उन दोनों के समानांतर एक रेखा है और उनके बीच में खींची गई है।
II. इस स्थान रेखा पर किसी भी बिंदु की दोनों मूल समानांतर रेखाओं से लंबवत दूरी समान होती है। आगे, इस स्थान रेखा के बाहर कोई भी बिंदु इस गुण को नहीं रखता।
उपर्युक्त में से कौन सा कथन सही है?
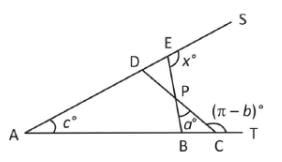
कोण x°, a°, c° और (π – b)° नीचे दिए गए चित्र में दर्शाए गए हैं। निम्नलिखित में से कौन सा सही है?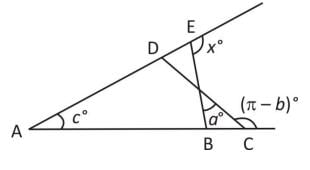
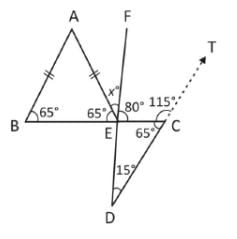
नीचे दिए गए चित्र में, AB, CD के समानांतर है। ∠ABC = 65°, ∠CDE = 15° और AB = AE है। ∠AEF का मान क्या है?
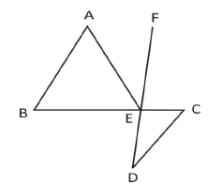
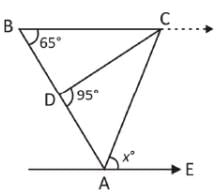
नीचे दिए गए चित्र में, ABC एक त्रिकोण है। BC, AE के समानांतर है। यदि BC = AC है, तो ∠CAE का मान क्या होगा?
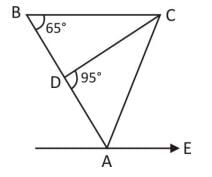



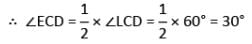
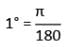
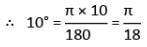
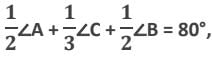 तब ∠C का मान क्या है?
तब ∠C का मान क्या है?