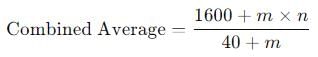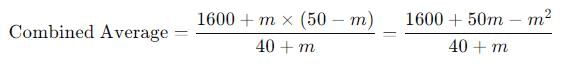अभ्यास परीक्षण: औसत - 1 - Bank Exams MCQ
15 Questions MCQ Test - अभ्यास परीक्षण: औसत - 1
एक बल्लेबाज़ का 25 पारियों के बाद औसत 56 रन था। यदि 26वीं पारी के बाद उसका औसत 2 रन बढ़ गया, तो 26वीं पारी में उसका स्कोर क्या था?
एक परिवार में 7 सदस्य हैं जिनकी औसत आयु 25 वर्ष है। राम, जो 12 वर्ष का है, परिवार में दूसरा सबसे छोटा है। राम के जन्म से पहले परिवार की औसत आयु कितनी थी?
10 छात्रों की कक्षा का औसत वजन 2 किलोग्राम बढ़ जाता है जब एक 30 किलोग्राम का छात्र निकलता है और दूसरा छात्र शामिल होता है। कुछ महीनों बाद, यह नया छात्र निकल जाता है और एक और छात्र शामिल होता है जिसका वजन उस छात्र से 10 किलोग्राम कम है जो अभी हाल ही में निकला। अंतिम और प्रारंभिक औसत के बीच का अंतर क्या है?
15 संख्याओं का औसत 18 है। यदि प्रत्येक संख्या को 9 से गुणा किया जाए, तो नए सेट की संख्याओं का औसत क्या होगा?
विराट कोहली द्वारा चार पारियों में औसत रन 48 हैं। पांचवीं पारी में, कोहली कुछ रन बनाते हैं, जिससे उनका औसत अब 60 हो जाता है। छठी पारी में वह अपनी पांचवीं पारी से 12 रन अधिक बनाते हैं और अब उनकी अंतिम पांच पारियों का औसत 78 हो जाता है। उसने अपनी पहली पारी में कितने रन बनाये? (वह किसी भी पारी में नॉटआउट नहीं रहते)
देव और ओम 22 छात्रों में से हैं जो एक परीक्षा लिखते हैं। देव का स्कोर 82.5 है। ओम के अलावा 21 छात्रों का औसत स्कोर 62 है। सभी 22 छात्रों का औसत स्कोर देव के अलावा 21 छात्रों के औसत स्कोर से एक अधिक है। ओम का स्कोर है।
20 छात्रों के एक समूह में एक परीक्षा के औसत अंक 4 से घट जाते हैं जब 90 अंक प्राप्त करने वाला शीर्ष छात्र एक नए छात्र से बदला जाता है। नए छात्र के कितने अंक थे?
तीन लड़कों, रॉस, जोई और चैंडलर का औसत वजन 74 किलोग्राम है। एक और लड़का, डेविड, समूह में शामिल होता है और औसत अब 70 किलोग्राम हो जाता है। यदि एक और लड़का, एरिक, जो डेविड से 3 किलोग्राम अधिक वजन वाला है, रॉस की जगह लेता है, तो जोई, चैंडलर, डेविड और एरिक का औसत वजन 75 किलोग्राम हो जाता है। रॉस का वजन क्या है?
सोमवार से बुधवार का औसत तापमान 35 °C था और मंगलवार से गुरुवार का औसत तापमान 30 °C था। यदि गुरुवार का तापमान सोमवार के तापमान का 1/2 था, तो गुरुवार का तापमान ______ था।
5 सदस्यों वाले परिवार की औसत आयु 20 वर्ष है। यदि सबसे छोटे सदस्य की आयु 10 वर्ष है, तो सबसे छोटे सदस्य के जन्म के समय परिवार की औसत आयु क्या थी?
10 पुरुषों का औसत वजन 2 किलोग्राम कम हो जाता है जब उनमें से एक, जिसका वजन 140 किलोग्राम है, को किसी अन्य व्यक्ति से बदल दिया जाता है। नए व्यक्ति का वजन ज्ञात करें।
पुरुषों के एक समूह की औसत आयु 6 वर्ष बढ़ जाती है जब 26 वर्ष का व्यक्ति 56 वर्ष के नए व्यक्ति से बदल दिया जाता है। समूह में कितने पुरुष हैं?
कक्षा का औसत वजन 54 किलोग्राम है। एक छात्र, जिसका वजन 145 किलोग्राम है, कक्षा में शामिल हुआ और अब कक्षा का औसत वजन 72 से कम एक प्रमुख संख्या बन जाता है। अब कक्षा में छात्रों की कुल संख्या ज्ञात कीजिए।
40 छात्रों की एक कक्षा पर विचार करें, जिनका औसत वजन 40 किलोग्राम है। इस कक्षा में m नए छात्र शामिल होते हैं, जिनका औसत वजन n किलोग्राम है। यदि यह ज्ञात है कि m + n = 50, तो अब कक्षा का अधिकतम संभावित औसत वजन क्या है?