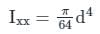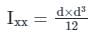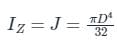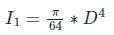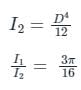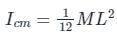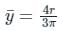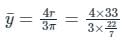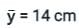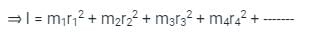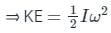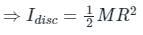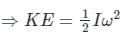Test: Moment of Inertia and Centroid - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Moment of Inertia and Centroid
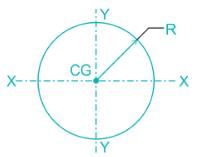
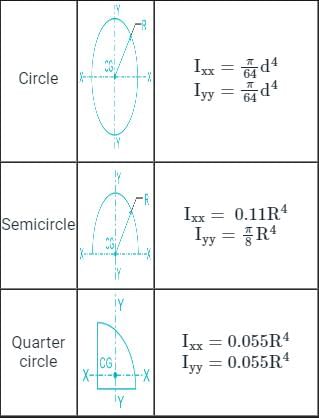
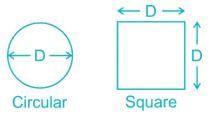
The ratio of moment of inertia of a circular plate to that of a square plate for equal depth is
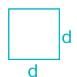
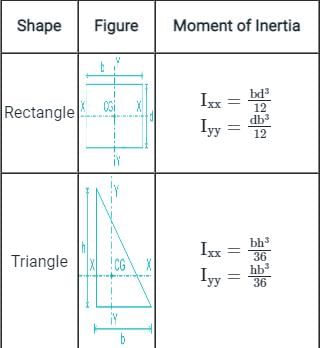
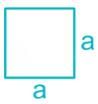
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is
The polar moment of inertia of a hollow circular shaft of outer diameter (D) and inner diameter (d) is
The ratio of the moment of inertia of a circular plate of diameter same as that of a side of a square plate is
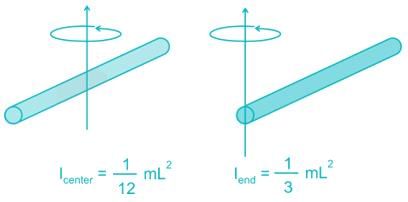
A thin rod of length L and mass M will have what moment of inertia about an axis passing through one of its edge and perpendicular to the rod?
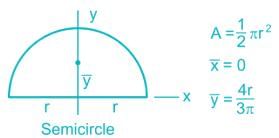
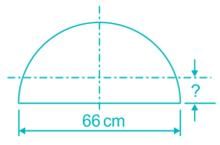
The CG of a semicircular plate of 66 cm diameter, from its base, is
Moment of inertia of a thin spherical shell of mass M and radius R, about its diameter is
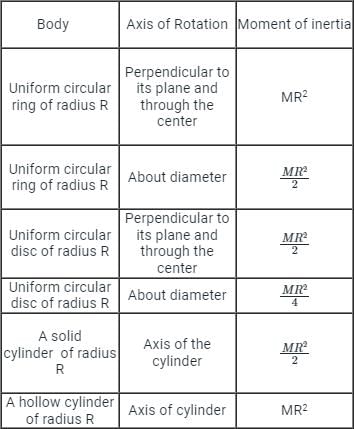
A thin disc and a thin ring, both have mass M and radius R. Both rotate about axes through their centre of mass and are perpendicular to their surfaces at the same angular velocity. Which of the following is true?
Point, where the total volume of the body is assumed to be concentrated is ______
The axis about which moment of area is taken is known as _____