Class 12 Exam > Class 12 Questions > During electrolysis of an aqueous solution of...
Start Learning for Free
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :
- a)1.2 L
- b)2.4 L
- c)2.6 L
- d)4.8 L
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L...
Equivalent of H2 = Equivalent of O2
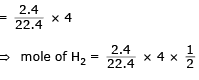
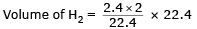
= 4.8 L
= 4.8 L
Most Upvoted Answer
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L...
Given:
Volume of oxygen liberated at anode = 2.4 L
STP conditions:
Temperature (T) = 273 K
Pressure (P) = 1 atm
To determine the volume of hydrogen liberated at the cathode, we need to use the concept of Faraday's laws of electrolysis.
1. Faraday's First Law of Electrolysis:
The mass of a substance liberated during electrolysis is directly proportional to the quantity of electricity passed through it.
2. Faraday's Second Law of Electrolysis:
The mass of different substances liberated by the same quantity of electricity is directly proportional to their chemical equivalent weights.
Using these laws, we can calculate the volume of hydrogen gas liberated at the cathode.
Step 1: Calculate the number of moles of oxygen gas liberated.
From the ideal gas equation, PV = nRT, we can calculate the number of moles of oxygen gas.
Given:
Volume of oxygen gas = 2.4 L
Pressure = 1 atm
Temperature = 273 K
R (Gas constant) = 0.0821 L.atm/mol.K
Using the formula: n = PV/RT
n = (1 atm * 2.4 L) / (0.0821 L.atm/mol.K * 273 K)
n = 0.1111 moles
Step 2: Calculate the number of moles of electrons passed.
Oxygen gas is formed by the reduction of water at the anode. The balanced equation is:
4OH- → 2H2O + O2 + 4e-
From the equation, we can see that for every mole of oxygen gas produced, 4 moles of electrons are passed. Therefore, the number of moles of electrons passed is 4 times the number of moles of oxygen gas.
Number of moles of electrons passed = 4 * 0.1111 moles = 0.4444 moles
Step 3: Calculate the number of moles of hydrogen gas liberated.
From the balanced equation of water electrolysis:
2H2O + 2e- → 2OH- + H2
We can see that for every 2 moles of electrons passed, 1 mole of hydrogen gas is liberated. Therefore, the number of moles of hydrogen gas liberated is half the number of moles of electrons passed.
Number of moles of hydrogen gas liberated = 0.4444 moles / 2 = 0.2222 moles
Step 4: Convert the number of moles of hydrogen gas to volume.
Using the ideal gas equation, PV = nRT, we can calculate the volume of hydrogen gas.
Given:
Pressure = 1 atm
Temperature = 273 K
Number of moles of hydrogen gas = 0.2222 moles
R (Gas constant) = 0.0821 L.atm/mol.K
Using the formula: V = nRT/P
V = (0.2222 moles * 0.0821 L.atm/mol.K * 273 K) / 1 atm
V = 4.8002 L
Therefore, the volume of hydrogen gas liberated at the cathode is approximately 4.8 L. Hence, the correct answer is option D.
Volume of oxygen liberated at anode = 2.4 L
STP conditions:
Temperature (T) = 273 K
Pressure (P) = 1 atm
To determine the volume of hydrogen liberated at the cathode, we need to use the concept of Faraday's laws of electrolysis.
1. Faraday's First Law of Electrolysis:
The mass of a substance liberated during electrolysis is directly proportional to the quantity of electricity passed through it.
2. Faraday's Second Law of Electrolysis:
The mass of different substances liberated by the same quantity of electricity is directly proportional to their chemical equivalent weights.
Using these laws, we can calculate the volume of hydrogen gas liberated at the cathode.
Step 1: Calculate the number of moles of oxygen gas liberated.
From the ideal gas equation, PV = nRT, we can calculate the number of moles of oxygen gas.
Given:
Volume of oxygen gas = 2.4 L
Pressure = 1 atm
Temperature = 273 K
R (Gas constant) = 0.0821 L.atm/mol.K
Using the formula: n = PV/RT
n = (1 atm * 2.4 L) / (0.0821 L.atm/mol.K * 273 K)
n = 0.1111 moles
Step 2: Calculate the number of moles of electrons passed.
Oxygen gas is formed by the reduction of water at the anode. The balanced equation is:
4OH- → 2H2O + O2 + 4e-
From the equation, we can see that for every mole of oxygen gas produced, 4 moles of electrons are passed. Therefore, the number of moles of electrons passed is 4 times the number of moles of oxygen gas.
Number of moles of electrons passed = 4 * 0.1111 moles = 0.4444 moles
Step 3: Calculate the number of moles of hydrogen gas liberated.
From the balanced equation of water electrolysis:
2H2O + 2e- → 2OH- + H2
We can see that for every 2 moles of electrons passed, 1 mole of hydrogen gas is liberated. Therefore, the number of moles of hydrogen gas liberated is half the number of moles of electrons passed.
Number of moles of hydrogen gas liberated = 0.4444 moles / 2 = 0.2222 moles
Step 4: Convert the number of moles of hydrogen gas to volume.
Using the ideal gas equation, PV = nRT, we can calculate the volume of hydrogen gas.
Given:
Pressure = 1 atm
Temperature = 273 K
Number of moles of hydrogen gas = 0.2222 moles
R (Gas constant) = 0.0821 L.atm/mol.K
Using the formula: V = nRT/P
V = (0.2222 moles * 0.0821 L.atm/mol.K * 273 K) / 1 atm
V = 4.8002 L
Therefore, the volume of hydrogen gas liberated at the cathode is approximately 4.8 L. Hence, the correct answer is option D.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer?
Question Description
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer?.
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer?.
Solutions for During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice During electrolysis of an aqueous solution of sodium sulphate if 2.4 L of oxygen at STP was liberated at anode. The volume of hydrogen at STP, liberated at cathode would be :a)1.2 Lb)2.4 Lc)2.6 Ld)4.8 LCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.













