Commerce Exam > Commerce Questions > Explain with numerical example that average c...
Start Learning for Free
Explain with numerical example that average cost is constant when marginal cost is equal to it?
Verified Answer
Explain with numerical example that average cost is constant when marg...
Following table considers a situation when MC = AC over a range of output. It is a situation of constant returns to a factor.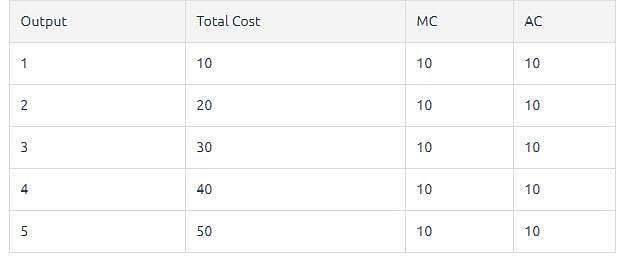

The table shows that when constant returns to a factor prevail over a range of output (1-5 units of output), MC remains constant. Consequently, TC increases at a constant rate and MC and AC are found to be equal to each other. In the entire range of output when AC = MC, AC is also found to be constant (like MC).
 This question is part of UPSC exam. View all Commerce courses
This question is part of UPSC exam. View all Commerce courses
Most Upvoted Answer
Explain with numerical example that average cost is constant when marg...
Introduction:
Average cost and marginal cost are important concepts in economics that help businesses determine their production decisions. Average cost is the total cost divided by the number of units produced, while marginal cost is the additional cost incurred by producing one additional unit. When marginal cost is equal to average cost, it implies that the average cost is constant. This can be explained using a numerical example.
Numerical Example:
Let's consider a hypothetical company that produces widgets. The total cost of producing different quantities of widgets is given below:
- Quantity (Q) = 1: Total Cost (TC) = $10
- Quantity (Q) = 2: Total Cost (TC) = $15
- Quantity (Q) = 3: Total Cost (TC) = $18
- Quantity (Q) = 4: Total Cost (TC) = $20
- Quantity (Q) = 5: Total Cost (TC) = $22
Calculating Marginal Cost:
To calculate marginal cost, we need to determine the change in total cost when one additional unit is produced. We can do this by subtracting the total cost of the previous quantity from the total cost of the current quantity.
- Marginal Cost (MC) = TC(Q) - TC(Q-1)
For example, the marginal cost of producing the second widget would be:
MC(Q=2) = TC(Q=2) - TC(Q=1)
= $15 - $10
= $5
Similarly, we can calculate the marginal cost for all the other quantities.
Calculating Average Cost:
Average cost is obtained by dividing the total cost by the quantity produced.
- Average Cost (AC) = TC(Q) / Q
For example, the average cost of producing the second widget would be:
AC(Q=2) = TC(Q=2) / Q
= $15 / 2
= $7.5
Similarly, we can calculate the average cost for all the other quantities.
Comparing Marginal Cost and Average Cost:
To determine if average cost is constant when marginal cost is equal to it, we need to compare the values of marginal cost and average cost at each quantity.
- Q = 1: MC(Q=1) = $10, AC(Q=1) = $10
- Q = 2: MC(Q=2) = $5, AC(Q=2) = $7.5
- Q = 3: MC(Q=3) = $3, AC(Q=3) = $6
- Q = 4: MC(Q=4) = $2, AC(Q=4) = $5
- Q = 5: MC(Q=5) = $2, AC(Q=5) = $4.4
Conclusion:
From the above comparison, we can see that when marginal cost is equal to average cost, the average cost remains constant. In our example, this occurs at a quantity of 5 widgets, where both marginal cost and average cost are $2. This implies that the additional cost of producing one more widget is equal to the average cost of all the widgets produced so far. When marginal cost is equal to average cost, it suggests that the firm is operating at its efficient scale, where it achieves optimal cost minimization.
Average cost and marginal cost are important concepts in economics that help businesses determine their production decisions. Average cost is the total cost divided by the number of units produced, while marginal cost is the additional cost incurred by producing one additional unit. When marginal cost is equal to average cost, it implies that the average cost is constant. This can be explained using a numerical example.
Numerical Example:
Let's consider a hypothetical company that produces widgets. The total cost of producing different quantities of widgets is given below:
- Quantity (Q) = 1: Total Cost (TC) = $10
- Quantity (Q) = 2: Total Cost (TC) = $15
- Quantity (Q) = 3: Total Cost (TC) = $18
- Quantity (Q) = 4: Total Cost (TC) = $20
- Quantity (Q) = 5: Total Cost (TC) = $22
Calculating Marginal Cost:
To calculate marginal cost, we need to determine the change in total cost when one additional unit is produced. We can do this by subtracting the total cost of the previous quantity from the total cost of the current quantity.
- Marginal Cost (MC) = TC(Q) - TC(Q-1)
For example, the marginal cost of producing the second widget would be:
MC(Q=2) = TC(Q=2) - TC(Q=1)
= $15 - $10
= $5
Similarly, we can calculate the marginal cost for all the other quantities.
Calculating Average Cost:
Average cost is obtained by dividing the total cost by the quantity produced.
- Average Cost (AC) = TC(Q) / Q
For example, the average cost of producing the second widget would be:
AC(Q=2) = TC(Q=2) / Q
= $15 / 2
= $7.5
Similarly, we can calculate the average cost for all the other quantities.
Comparing Marginal Cost and Average Cost:
To determine if average cost is constant when marginal cost is equal to it, we need to compare the values of marginal cost and average cost at each quantity.
- Q = 1: MC(Q=1) = $10, AC(Q=1) = $10
- Q = 2: MC(Q=2) = $5, AC(Q=2) = $7.5
- Q = 3: MC(Q=3) = $3, AC(Q=3) = $6
- Q = 4: MC(Q=4) = $2, AC(Q=4) = $5
- Q = 5: MC(Q=5) = $2, AC(Q=5) = $4.4
Conclusion:
From the above comparison, we can see that when marginal cost is equal to average cost, the average cost remains constant. In our example, this occurs at a quantity of 5 widgets, where both marginal cost and average cost are $2. This implies that the additional cost of producing one more widget is equal to the average cost of all the widgets produced so far. When marginal cost is equal to average cost, it suggests that the firm is operating at its efficient scale, where it achieves optimal cost minimization.
Attention Commerce Students!
To make sure you are not studying endlessly, EduRev has designed Commerce study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Commerce.

|
Explore Courses for Commerce exam
|

|
Similar Commerce Doubts
Explain with numerical example that average cost is constant when marginal cost is equal to it?
Question Description
Explain with numerical example that average cost is constant when marginal cost is equal to it? for Commerce 2024 is part of Commerce preparation. The Question and answers have been prepared according to the Commerce exam syllabus. Information about Explain with numerical example that average cost is constant when marginal cost is equal to it? covers all topics & solutions for Commerce 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Explain with numerical example that average cost is constant when marginal cost is equal to it?.
Explain with numerical example that average cost is constant when marginal cost is equal to it? for Commerce 2024 is part of Commerce preparation. The Question and answers have been prepared according to the Commerce exam syllabus. Information about Explain with numerical example that average cost is constant when marginal cost is equal to it? covers all topics & solutions for Commerce 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Explain with numerical example that average cost is constant when marginal cost is equal to it?.
Solutions for Explain with numerical example that average cost is constant when marginal cost is equal to it? in English & in Hindi are available as part of our courses for Commerce.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Here you can find the meaning of Explain with numerical example that average cost is constant when marginal cost is equal to it? defined & explained in the simplest way possible. Besides giving the explanation of
Explain with numerical example that average cost is constant when marginal cost is equal to it?, a detailed solution for Explain with numerical example that average cost is constant when marginal cost is equal to it? has been provided alongside types of Explain with numerical example that average cost is constant when marginal cost is equal to it? theory, EduRev gives you an
ample number of questions to practice Explain with numerical example that average cost is constant when marginal cost is equal to it? tests, examples and also practice Commerce tests.

|
Explore Courses for Commerce exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























