Class 9 Exam > Class 9 Questions > Explain the 5th postulate of EUCLID S GEOMETR...
Start Learning for Free
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE
Most Upvoted Answer
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE
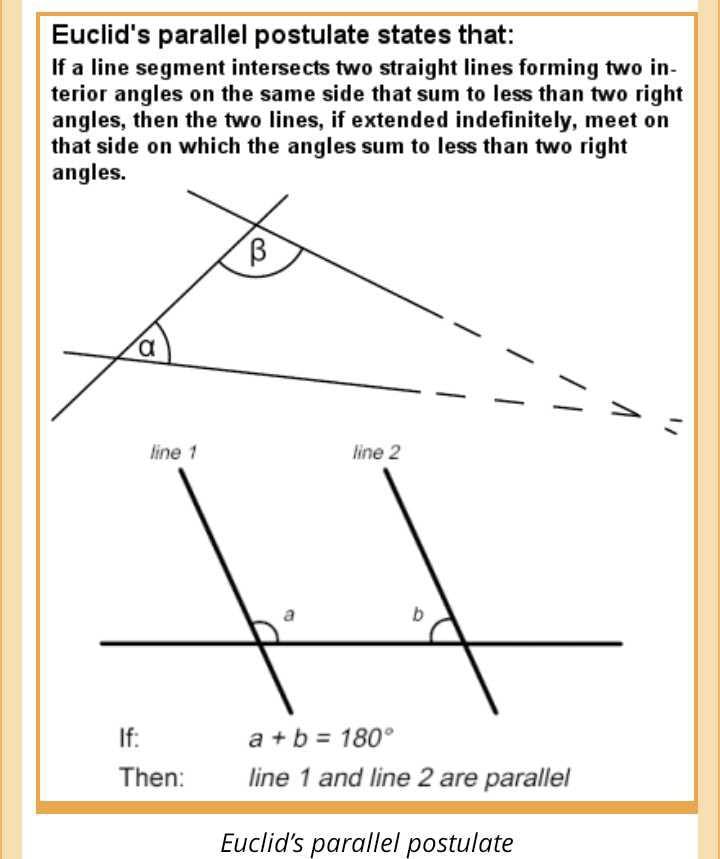
Community Answer
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE
The 5th Postulate of Euclid's Geometry
The 5th postulate of Euclid's geometry, also known as the parallel postulate, is one of the axioms that Euclid used to develop his system of geometry. It states that if there is a line and a point not on that line, then there is exactly one line through the given point that is parallel to the given line. This postulate is essential in the study of parallel lines and forms the basis for many geometric proofs and theorems. Let's break down this postulate and understand it in simple terms:
Key Points:
- Euclid's geometry is a mathematical system developed by the ancient Greek mathematician Euclid around 300 BCE.
- The 5th postulate, also known as the parallel postulate, states that if there is a line and a point not on that line, then there is exactly one line through the given point that is parallel to the given line.
Understanding the Postulate:
To understand the 5th postulate, let's imagine a scenario where we have a line (let's call it Line A) and a point outside that line (let's call it Point P). According to the postulate, there will be exactly one line (let's call it Line B) passing through Point P that does not intersect Line A.
Implications of the Postulate:
This postulate has several implications and consequences in geometry:
1. Parallel Lines: The postulate allows us to define what parallel lines are. Two lines are considered parallel if they never intersect, and this postulate guarantees the existence of such lines.
2. Parallel Line Theorems: The postulate forms the basis for various theorems involving parallel lines, such as the alternate interior angles theorem, corresponding angles theorem, and the transversal property.
3. Constructing Parallel Lines: Using the postulate, we can construct parallel lines given a point and a line. By drawing a line through the given point and ensuring it never intersects the given line, we create a parallel line.
4. Proving Geometric Theorems: The 5th postulate is often used as a starting point in geometric proofs to establish the existence of parallel lines, which in turn helps prove other theorems and properties.
5. Non-Euclidean Geometry: The 5th postulate was heavily studied and questioned by mathematicians, leading to the development of non-Euclidean geometries, where the parallel postulate is modified or replaced by alternative statements.
Conclusion:
The 5th postulate, or the parallel postulate, is a fundamental axiom in Euclid's geometry. It states that if a line and a point not on that line are given, there exists exactly one line through the point that is parallel to the given line. This postulate has significant implications in the study of parallel lines and forms the foundation for various theorems and geometric proofs.
The 5th postulate of Euclid's geometry, also known as the parallel postulate, is one of the axioms that Euclid used to develop his system of geometry. It states that if there is a line and a point not on that line, then there is exactly one line through the given point that is parallel to the given line. This postulate is essential in the study of parallel lines and forms the basis for many geometric proofs and theorems. Let's break down this postulate and understand it in simple terms:
Key Points:
- Euclid's geometry is a mathematical system developed by the ancient Greek mathematician Euclid around 300 BCE.
- The 5th postulate, also known as the parallel postulate, states that if there is a line and a point not on that line, then there is exactly one line through the given point that is parallel to the given line.
Understanding the Postulate:
To understand the 5th postulate, let's imagine a scenario where we have a line (let's call it Line A) and a point outside that line (let's call it Point P). According to the postulate, there will be exactly one line (let's call it Line B) passing through Point P that does not intersect Line A.
Implications of the Postulate:
This postulate has several implications and consequences in geometry:
1. Parallel Lines: The postulate allows us to define what parallel lines are. Two lines are considered parallel if they never intersect, and this postulate guarantees the existence of such lines.
2. Parallel Line Theorems: The postulate forms the basis for various theorems involving parallel lines, such as the alternate interior angles theorem, corresponding angles theorem, and the transversal property.
3. Constructing Parallel Lines: Using the postulate, we can construct parallel lines given a point and a line. By drawing a line through the given point and ensuring it never intersects the given line, we create a parallel line.
4. Proving Geometric Theorems: The 5th postulate is often used as a starting point in geometric proofs to establish the existence of parallel lines, which in turn helps prove other theorems and properties.
5. Non-Euclidean Geometry: The 5th postulate was heavily studied and questioned by mathematicians, leading to the development of non-Euclidean geometries, where the parallel postulate is modified or replaced by alternative statements.
Conclusion:
The 5th postulate, or the parallel postulate, is a fundamental axiom in Euclid's geometry. It states that if a line and a point not on that line are given, there exists exactly one line through the point that is parallel to the given line. This postulate has significant implications in the study of parallel lines and forms the foundation for various theorems and geometric proofs.

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE
Question Description
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE.
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE for Class 9 2025 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE covers all topics & solutions for Class 9 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE.
Solutions for Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE defined & explained in the simplest way possible. Besides giving the explanation of
Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE, a detailed solution for Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE has been provided alongside types of Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE theory, EduRev gives you an
ample number of questions to practice Explain the 5th postulate of EUCLID S GEOMETRY IN SIMPLE LANGUAGE tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























