Class 9 Exam > Class 9 Questions > ABC is a triangle. The bisector of the exteri...
Start Learning for Free
ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A.
? Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)
Verified Answer
ABC is a triangle. The bisector of the exterior angle at B and the bis...
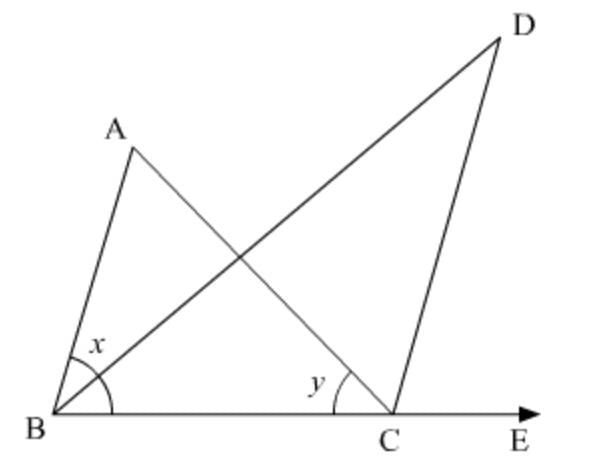
Here, given :-
ABC is a triangle.
BD is the interior angle bisector of ∠B and CD is the exterior angle bisector of ∠C.
To prove that :- BDC =1/2 angle A.
proof :- In ΔABC
∠A + ∠B + ∠C = 180degree
⇒ ∠A = 180degree – x – y .... (1)
and In ΔBDE
angle B = x / 2
angle c= y + 180- y/2= 180+y/2
and , therefore angle b + c + d = 180degree
so, angle D = 180degree- x /2 - 180+y/2
= 180 - x - y /2 ....( 2 )
Now from eqation ( 1 ) and ( 2 ), we get the result..
angle D = angle A / 2... (ANS)...
 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
ABC is a triangle. The bisector of the exterior angle at B and the bis...
Proof:
Given: ABC is a triangle, the bisector of the exterior angle at B and the bisector of angle C intersect each other at D.
To Prove: Angle D is equal to half angle A.
Proof:
Step 1: Draw a rough sketch of triangle ABC.
Step 2: Label the given points and angles on the sketch.
- Let ∠A be the angle at vertex A.
- Let ∠B be the angle at vertex B.
- Let ∠C be the angle at vertex C.
- Let ∠D be the angle at vertex D.
Step 3: Use the Angle Bisector Theorem to establish a relationship between the angles.
Step 3a: The Angle Bisector Theorem states that the angle bisector of an angle in a triangle divides the opposite side into two segments that are proportional to the lengths of the other two sides.
Step 3b: Since D is the intersection point of the bisector of the exterior angle at B and the bisector of angle C, we can conclude that D is the angle bisector of both the exterior angle at B and angle C.
Step 3c: Therefore, we can apply the Angle Bisector Theorem to triangle ABC with respect to angle A and angle B.
Step 3d: According to the Angle Bisector Theorem, we have:
AB/BD = AC/CD
Step 3e: Rearrange the equation to isolate AB:
AB = (BD * AC) / CD
Step 4: Use the Converse of the Angle Bisector Theorem to establish an equality between angles A and D.
Step 4a: The Converse of the Angle Bisector Theorem states that if a line divides two sides of a triangle proportionally, then it is an angle bisector.
Step 4b: Since we have established that D is the angle bisector of both the exterior angle at B and angle C, we can conclude that D is also the angle bisector of angle A.
Step 4c: Therefore, angle D is equal to half of angle A.
Step 5: Thus, we have proved that angle D is equal to half of angle A in triangle ABC.
Given: ABC is a triangle, the bisector of the exterior angle at B and the bisector of angle C intersect each other at D.
To Prove: Angle D is equal to half angle A.
Proof:
Step 1: Draw a rough sketch of triangle ABC.
Step 2: Label the given points and angles on the sketch.
- Let ∠A be the angle at vertex A.
- Let ∠B be the angle at vertex B.
- Let ∠C be the angle at vertex C.
- Let ∠D be the angle at vertex D.
Step 3: Use the Angle Bisector Theorem to establish a relationship between the angles.
Step 3a: The Angle Bisector Theorem states that the angle bisector of an angle in a triangle divides the opposite side into two segments that are proportional to the lengths of the other two sides.
Step 3b: Since D is the intersection point of the bisector of the exterior angle at B and the bisector of angle C, we can conclude that D is the angle bisector of both the exterior angle at B and angle C.
Step 3c: Therefore, we can apply the Angle Bisector Theorem to triangle ABC with respect to angle A and angle B.
Step 3d: According to the Angle Bisector Theorem, we have:
AB/BD = AC/CD
Step 3e: Rearrange the equation to isolate AB:
AB = (BD * AC) / CD
Step 4: Use the Converse of the Angle Bisector Theorem to establish an equality between angles A and D.
Step 4a: The Converse of the Angle Bisector Theorem states that if a line divides two sides of a triangle proportionally, then it is an angle bisector.
Step 4b: Since we have established that D is the angle bisector of both the exterior angle at B and angle C, we can conclude that D is also the angle bisector of angle A.
Step 4c: Therefore, angle D is equal to half of angle A.
Step 5: Thus, we have proved that angle D is equal to half of angle A in triangle ABC.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)?
Question Description
ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)?.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)?.
Solutions for ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? defined & explained in the simplest way possible. Besides giving the explanation of
ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)?, a detailed solution for ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? has been provided alongside types of ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? theory, EduRev gives you an
ample number of questions to practice ABC is a triangle. The bisector of the exterior angle at B and the bisector of angle C intersect each other at D.Prove that angle D equal to half angle A. Related: त्रिभुज (भाग-1) - गणित (कक्षा 9)? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























