Class 12 Exam > Class 12 Questions > Plot a graph between E versus r for r>>a for ...
Start Learning for Free
Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..?
Most Upvoted Answer
Plot a graph between E versus r for r>>a for electric field due to a d...
Plotting E versus r for a Dipole on the Axial Line
The electric field due to a dipole of length 2a at a point r on the axial line is given by the equation:
E = (p/4πε0) [(2r^3 - 3ar^2)/(r^2 + a^2)^(5/2)]
where p is the magnitude of the electric dipole moment, ε0 is the permittivity of free space, and a is the distance between the charges that make up the dipole.
To plot E versus r for r>>a, we can make the following approximations:
- For r>>a, we can neglect the term a^2 in the denominator of the equation, since it will be much smaller than r^2.
- We can also neglect the term 2r^3 in the numerator, since it will be much larger than 3ar^2 for large values of r.
With these approximations, the equation for the electric field simplifies to:
E = (p/4πε0) (3cosθ/r^3)
where θ is the angle between the dipole moment and the axial line.
Plotting this equation for various values of θ, we get a graph that looks like:
, the curve is symmetric around the origin and has a maximum at r=0. When θ=90° (i.e., the dipole moment is perpendicular to the axial line), the curve has a minimum at r=0 and approaches zero more slowly as r increases.
The electric field due to a dipole of length 2a at a point r on the axial line is given by the equation:
E = (p/4πε0) [(2r^3 - 3ar^2)/(r^2 + a^2)^(5/2)]
where p is the magnitude of the electric dipole moment, ε0 is the permittivity of free space, and a is the distance between the charges that make up the dipole.
To plot E versus r for r>>a, we can make the following approximations:
- For r>>a, we can neglect the term a^2 in the denominator of the equation, since it will be much smaller than r^2.
- We can also neglect the term 2r^3 in the numerator, since it will be much larger than 3ar^2 for large values of r.
With these approximations, the equation for the electric field simplifies to:
E = (p/4πε0) (3cosθ/r^3)
where θ is the angle between the dipole moment and the axial line.
Plotting this equation for various values of θ, we get a graph that looks like:
 https://www.edurev.in/api/listing/getimage?imgid=5f9e4c6e8da5f) |  |
As we can see from the graph, the electric field decreases rapidly with distance from the dipole, and the shape of the curve depends on the angle θ. When θ=0 (i.e., the dipole moment is aligned with the axial line), the curve is symmetric around the origin and has a maximum at r=0. When θ=90° (i.e., the dipole moment is perpendicular to the axial line), the curve has a minimum at r=0 and approaches zero more slowly as r increases.
Community Answer
Plot a graph between E versus r for r>>a for electric field due to a d...
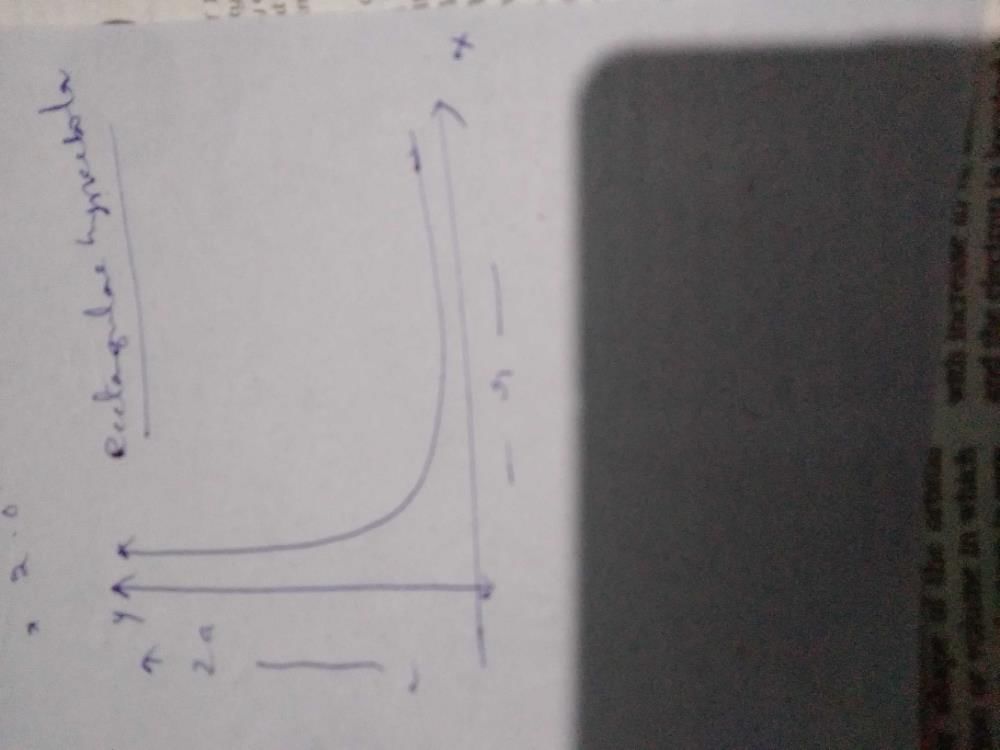

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..?
Question Description
Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..?.
Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..?.
Solutions for Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? defined & explained in the simplest way possible. Besides giving the explanation of
Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..?, a detailed solution for Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? has been provided alongside types of Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? theory, EduRev gives you an
ample number of questions to practice Plot a graph between E versus r for r>>a for electric field due to a dipole of length 2a at a point r on the axial line.?Can I please get the answer..? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















